Яков Гегузин - Капля

Теперь о полете маленькой капли, которая, падая, со­храняет форму шарика. Если с ее формой ничего не проис­ходит и шарик остается шариком, то о движении капли лучше говорить так: воздух, двигаясь снизу вверх, вязко обтекает водяной шарик. Попробуем вычислить скорость, с которой при этом водяной шарик — капля — прибли­жается к земле.

Начнем с примера, который имеет прямое отношение к нашей задаче о вязком обтекании воздухом капли. Допу­стим, к нити из вязкого вещества — смолы или разогре­того стекла — прикреплен грузик, под действием которого нить будет удлиняться, вязко течь. Очевидно, ее удлине­ние ( Δ l ) будет тем большим, чем длиннее нить ( l ), больше время течения ( t ), больше нагрузка, приложенная к нити ( Р ), и меньше вязкость ( η ) вещества, из которого она изго­товлена. Сказанное можно записать в виде формулы

Δ l = lPt / η ,

из которой следует, что скорость удлинения υ = Δ l / t = lP / η

Возвратимся теперь к вопросу о вязком обтекании воздухом капли-шарика. Этот процесс должен подчиняться тому же закону, что и вязкое течение нити. Различие заключается лишь в том, что в одном случае течет смола или стекло, а в другом — воздух. Важно, что в обоих случа­ях имеет место вязкое течение. Обратим, однако, внимание на то, что в интересующей нас задаче характерный раз­мер — не длина нити, а радиус шарика R и что напряже­ние Р пропорционально отношению силы F , тянущей шарик, к площади его сечения, т. е Р≈F/πR 2 . Применительно к шарику формулу, определяющую скорость, можно переписать в виде: υ ≈ F / R η . Мы воспользовались знаком «про­порционально» потому, что не учли конкретной геометрии потока воздуха вокруг шарика. Точный расчет приводит к формуле, которая от нашей отличается лишь множите­лем 1 / 6 . π , и таким образом:

υ = F / 6π R η

Обсудим величину F .

Если бы шарик падал в вакууме, то

F = F ↓ = mg = 4/ 3 π R 3 ρ g .

Так как шарик находится в воздухе, то на него действует и архимедова сила F↑ , кото­рая направлена противоположно F↓ и определяется той же формулой, что и F↓ , только величину ρ — плотность вещества шарика нужно заменить величиной ρ o — плот­ностью воздуха. Вот теперь можно записать интересую­щую нас формулу в окончательном виде:

υ = 1( F↓ - F↑) /6π R η = 2/ 9 .g R 2. (ρ - ρ o)/ η

Эту формулу называют формулой Стокса. Нам она позже понадобится.

Вычислим скорость падения маленькой дождевой кап­ли. Допустим, что ее размер R ≈ 10 -1см. Так как g ≈ 10 3см/сек 2, η ≈ 2 . 10 -2г/см .сек (пуаз), ρ = 1 г/см 3, ρ o = 1,2 .10 -3г/см 3, то υ ≈ 10 2см/сек.

Итак, мы выяснили, что маленькие капли летят со ско­ростью, пропорциональной квадрату их радиуса, и что величина этой скорости порядка 100 см за секунду. Если маленькая капля зародилась в облаке, которое плавает над землей на высоте около километра, и если ничто не помешает ей себя сохранить в полете, до земли ей лететь долго — около 15 мин. Еще раз подчеркнем — расска­занное о маленькой дождевой капле справедливо при соблюдении очень важной оговорки: если капля сохра­нит себя в целости на протяжении всего времени полета от облака до земли. И еще одна оговорка: все рассказан­ное о скорости полета капли относится к установившему­ся, или, как говорят физики, стационарному, режиму. В са­мом начале полета капля двигалась ускоренно, пока не достигла стационарной скорости.

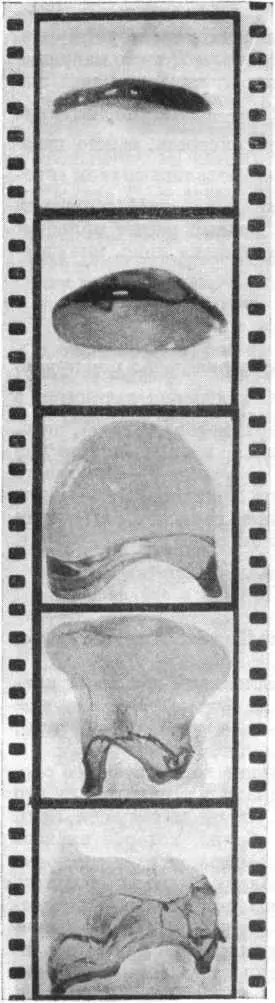
Так во время полета изменяется форма крупной капли, падающей в воздухе

Теперь о больших каплях. Речь идет о каплях крупных, размер которых достигает не­скольких миллиметров. Та­кие капли иногда образуются в искусственных условиях, например при распаде струй, а иногда и в условиях есте­ственного дождя. С ними про­исходит вот что.

Большая капля, встречая при падении сопротивление воздуха, расплющивается ( Р υ >> Р л !!!). Плоская водя­ная лепешка, летящая в воз­духе, надувается им и стано­вится подобна парашюту. По мере того как этот миниатюр­ный водяной парашютик раз­дувается воздухом, образую­щая его пленка становится все тоньше и в конце концов рвется, прокалывается воз­душной струей. И тогда она распадается на мелкие капли, у которых уже своя судьба.