Яков Гегузин - Живой кристалл

Воспользуемся нашей ниточкой и обсудим некоторые взаимопревращения дефектов, наблюдающиеся и в реальных кристаллах, и с помощью моделей, в частности модели БНЛ. Вначале о ситуациях безоговорочно выгодных, когда дефект исчезает. Например: избыточные вакансии исчезают во внутренних границах. Встретившись с границей (или вакансия подошла к границе, или граница подошла к вакансии), вакансия может в ней исчезнуть. Это означает: была и нет! Для вакансии это событие по меньшей мере серьезное: она погибла! Связанная с ней энергия выделилась. А для границы, поглотившей вакансию, это вообще не событие, так как, поглотив «атом пустоты», граница своей структуры, а следовательно, и энергии не меняет. Процесс безоговорочно выгодный: выигрыш есть, проигрыша нет! Очень легко этот процесс наблюдается с помощью модели БНЛ: граница движется и, оставаясь самой собой, сметает встретившуюся у нее на пути вакансию.

В иной ситуации судьба вакансии может постичь границу в целом: она тоже может исчезнуть. Представьте себе, что граница замкнута, что она ограничивает собой блок в кристалле. К замкнутой, а следовательно, и искривленной границе будет приложена сила, обусловленная лапласовским давлением. Она вынудит границу двигаться так, чтобы ее протяженность уменьшилась вплоть до исчезновения. С помощью кинокамеры в модели БНЛ исчезновение замкнутых границ наблюдается отчетливо. Об этом свидетельствует приводимая кинограмма.

Теперь о взаимодействиях, выгодность которых не очевидна. Обсудим их на примере дислокаций. Если дислокации находятся в одной плоскости скольжения и их векторы Бюргерса ориентированы противоположно, им выгодно притянуться друг к другу и, встретившись, исчезнуть, аннигилировать. Если каждая из них имела единичную длину и, следовательно, в ней была запасена энергия ≈ Gb 2 , их аннигиляция будет сопровождаться излучением энергии ≈ 2 Gb 2≈ 2• 10 -3эрг.

Если же векторы Бюргерса ориентированы параллельно, то такие дислокации будут друг от друга отталкиваться.

Убедимся в этом, следуя за путеводной ниточкой. Если бы такие дислокации слились, они образовали бы одну дислокацию с удвоенной величиной вектора Бюргерса ,т. е. с энергией

W 2≈ G (2 b) 2= 4 Gb 2 .

А будучи разобщенными, они имели бы энергию

W 1 ≈ Gb 2+ Gb 2= 2 Gb 2 .

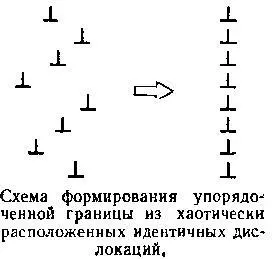
Так как W 2 > W 1 , объединение невыгодно, выгодно отталкивание. А вот если бы такие дислокации находились не в одной, а в параллельных плоскостях скольжения, то, начиная с некоторого расстояния между плоскостями, могло бы оказаться оправданным притяжение дислокаций. При этом они расположились бы одна под другой в связи с тем, что область сжимающих напряжений вблизи одной дислокации частично перекрылась бы с областью растягивающих напряжений вблизи другой дислокации (помните модельный опыт с резиновым жгутом?), и оказалось бы, что W 2 < W 1 . Выгодно! Последний случай очень важен для судьбы кристалла. Множество разрозненных идентичных дислокаций, расположившись друг над другом, образуют упорядоченную дислокационную стенку, ансамбль взаимодействующих дислокаций образует границу. Этой возможностью кристалл пользуется очень широко: если в нем поселено множество дислокаций, он предпочтет, упорядочив их расположения, превратиться в мозаичный кристалл. Все по тем же термодинамическим соображениям: выгодно!

Перед глазами читателя я лишь чуть-чуть приоткрыл завесу, за которой — огромная проблема «взаимодействие и взаимопревращение дефектов в кристалле». Именно так: чуть-чуть, в мере, необходимой для того, чтобы к эскизному портрету живого кристалла добавить еще одну черту.

Рассуждая о далеком прошлом естественных кристаллов, замечательный польский поэт Юлиан Тувим писал: