Яков Гегузин - Живой кристалл

Теория Борна, математически стройная и внутренне непротиворечивая, подтверждалась многими экспериментами. Сопоставляя ее следствия с экспериментально установленными фактами, Борн объяснил оптические, электрические и многие другие свойства ионных структур. В противоречии с его теорией оказались лишь данные о прочности кристаллов. Известно было, что, например, кристалл каменной соли разрушается, если к нему приложить напряжение σ≈ 4,5• 10 7дин/см 2, а точный и последовательный расчет теоретика предсказывал существенно иную величину: σ≈ 2• 10 10дин/см 2.

Сохранив идею, упростим расчет Борна и попытаемся примитивно оценить величину прочности кристалла. Борн ее вычислил строго.

Мы знаем, что прочность кристалла есть отношение силы, которую нужно приложить, чтобы его разорвать, к площади поверхности, по которой разрыв произошел: σ = F/S

Простота и очевидность сделанной оценки не должны в глазах читателя умалить проницательность теоретика. Нам, полвека спустя, легко и просто быть умеющими и понимающими, за нами величие Борна, который в 1915 г., не имея предшественников, мыслил независимо и революционно. Он был великим мастером. Здесь я хочу обратить внимание читателя на то, что в приведенном расчете, относящемся к разрыву кристалла, как и в расчете Френкеля, относившемся к сдвигу, делается все то же «классическое» предположение, что все связи рвутся одновременно.

Осмысливая противоречия между расчетом Борна и экспериментальными данными, Иоффе должен был обсуждать две возможности: либо теоретик ошибся, либо эксперименты неточны! Второе предположение следует отбросить, не колеблясь, потому что, даже если бы произошло невероятное и экспериментаторы ошиблись в 500 раз, их поправила бы многовековая практика обращения человека с кристаллами NаС1. Ведь если бы действительно их прочность была в согласии с теорией Борна, то не так просто было бы добыть в штольне соляную глыбу, орудуя киркой, и непростой была бы задача истолочь эту глыбу в порошок. В 500 раз экспериментаторы не могли ошибиться! И теоретик вряд ли ошибался так сильно: и мысли его логичны, и многие иные факты, следуя этим же мыслям, он объяснил очень успешно.

Правду следовало искать где-то в другом месте. Именно это и сделал Иоффе. Он рассуждал так: Борн, конечно же не ошибается, но рассчитывает он идеальную ситуацию когда одновременно рвутся все п связей. А если они рвутся не одновременно? Тогда, очевидно, разрушение будет происходить не мгновенно, так как связи рвутся последовательно, и при напряжении, значительно меньшем того, которое следует из теории.

Иоффе предположил, что на поверхности кристалла имеются микроскопические трещины. При нагрузках, меньших соответствующей «теоретической» прочности в устье трещины, в маленьком объеме кристалла могут возникнуть напряжения, при которых связи начнут рваться. А это значит, что трещина будет распространяться в глубь образца, пронижет его и расчленит на две части. Кристалл разрушится не потому, что в плоскости разрыва одновременно разрушились все связи, а потому, что последовательно разрушающиеся связи дали возможность трещине вырасти и расчленить кристалл.

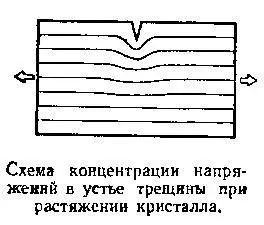
В то время, когда Иоффе осмысливал свои опыты, идея «трещины» носилась в воздухе. И не случайно почти одновременно была использована и Гриффитсом, и Иоффе.

То, о чем думал Иоффе, представляя механизм разрушения, можно отчетливо проиллюстрировать модельным опытом. Он прост, и его результаты не оставляют сомнений. На предметном столике микроскопа растягивается тонкая пластинка плексигласа, на боковом торце которой сделан острый и неглубокий надрез. Пластинка моделирует кристалл, надрез — трещину на его поверхности. В поляризованном свете можно отличить напряженные участки в плексигласе: чем больше напряжение, тем соответствующий участок темнее. Так вот, на последовательности кадров отснятого нами кинофильма видно, что в устье надреза напряжения максимальны и что пластинка разрушается вследствие движения напряженного устья надреза сквозь нее. Происходит это при напряжениях, значительно меньших тех, которые необходимы для разрушения пластинки без надреза.