Сергей Суворов - О чем рассказывает свет

Последуем за рассуждениями ученых и попробуем разобраться в механизме появления интерференции. Нарисуем в проекции непрозрачную пластинку с двумя щелями А 1 и А 2 и проходящие сквозь них одноцветные лучи 1 и 2 (рис. 12). Оба интерферирующих луча мы берем параллельными; это значит, что геометрическое пересечение их возможно только на бесконечно большом расстоянии. Но с помощью системы линз можно свести эти лучи в одну точку на близком расстоянии (как это осуществляется, мы здесь рассматривать не будем). Расстояние между щелями (а значит, и между лучами) и ширина щелей на рисунке для ясности чрезмерно увеличены; на самом деле они очень малы, порядка тысячных долей миллиметра. Направление лучей мы измеряем углом между лучами и перпендикуляром к непрозрачной пластинке со щелями и обозначаем этот угол греческой буквой φ 1 (фи).

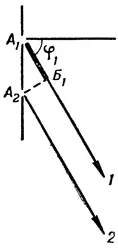
Рис. 12. Определение разности хода волн двух параллельных лучей

Ясно, что до взаимной встречи луч 1 должен будет пройти путь больший, чем луч 2 , а именно на величину, которая на рисунке обозначена буквами А 1Б 1 . Пусть у этих лучей разность хода волн в точках А 1 и А 2 равна нулю. Когда волны света, идущие вдоль луча 1 , достигнут точки Б 1 образуется разность хода волн (по отношению к волнам, идущим вдоль луча 2 ). Она будет равна отрезку А 1Б 1 .

Что будет на экране в результате взаимодействия лучей, идущих в указанном направлении под углом φ 1 — усилится яркость света или, напротив, он погаснет?

Это зависит от величины разности хода волн, выражаемой отрезком А 1Б 1 . Если отрезок А 1Б 1 равен целому числу волн (0, λ , 2 λ , З λ , 4 λ и т. д.), то в направлении под углом φ 1 будет усиление света. Если же отрезок А 1Б 1 равен целому числу волн с половиной (λ /2, 1 1/2 λ , 2 1/2 λ и т. д.), то в направлении φ 1 лучи погасят друг друга.

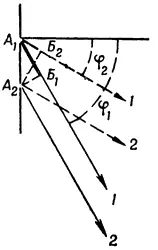
Рис. 13. Зависимость разности хода волн от угла отклонения лучей

Если мы будем рассматривать другую пару интерферирующих лучей, идущих под углом φ 2 , то длина отрезка А 1Б 1 т. е. разность хода волн, будет уже другой; это ясно видно на рис. 13 : А 1Б 1 не равно А 1Б 2 .

Будем последовательно рассматривать пары интерферирующих лучей, начиная с тех, которые идут под углом, равным нулю.

Ясно, что разность хода волн у этой первой пары лучей равна нулю; они усилят друг друга, на экране появится цветная яркая полоса. По мере увеличения угла отклонения лучей разность хода волн будет возрастать и приближаться к λ /2, яркость света в этих направлениях будет постепенно ослабляться. Когда при некотором угле разность хода волн достигнет λ /2, лучи в этом направлении погасят друг друга, на экране будет темная полоса.

При дальнейшем увеличении угла разность хода волн будет возрастать от λ /2 и выше. Яркость освещения в соответствующих местах экрана будет постепенно увеличиваться. Она будет наибольшей, когда разность хода волн достигнет λ . Далее при возрастании угла разность хода волн будет возрастать от λ и выше; когда она достигнет 1 1/2 λ на экране снова появится темная полоса.

Так, при возрастании наклона лучей разность хода волн у пары соседних лучей будет поочередно равна 0, λ /2, 1 λ , 1 1/2 λ , 2 λ, 2 1/2 λ и т. д., а на экране в соответствующих направлениях будут перемежаться цветные и темные полосы.

Если мы будем освещать щели другими одноцветными лучами, то у них наклон лучей, дающих первую темную полосу, будет уже не тот, что у лучей первого цвета. Это происходит потому, что у них другая длина волны; поэтому отрезок, равный разности хода в полуволну, будет уже не А 1Б 1 , а какой-то другой.

Так представляют себе физики механизм появления световой интерференции.

Опыт с интерференцией света замечателен не только тем, что он свидетельствует о наличии у света волновых свойств, он дает возможность измерить и длину волны интерферирующего света.

Рассмотрим на экране (рис. 14) те цветные полосы, в которых лучи света усиливают друг друга, т. е. где образуются «максимумы света». Одна из цветных полос по перпендикуляру от щели будет наиболее яркой; она образуется от лучей, которые идут после прохождения щелей под углом φ 1 равным нулю. Физики назвали эту яркую цветную полосу «максимумом нулевого порядка». По обе стороны от нее будут цветные полосы одинаковой яркости, но послабее, чем максимум нулевого порядка. Это — максимумы первого порядка.