Марио Бертолотти - История лазера

Свойства солитонов и их взаимодействие делает такие импульсы пригодными, в частности, для создания таких устройств, как световые переключатели, ответвители; их, тем самым, можно использовать для передачи в оптических волокнах. В будущем солитоны могут составить основные элементы оптических компьютеров.

Теперь мы рассмотрим одно из наиболее курьезных и интригующих применений лазеров, квантовой оптики и квантовой механики: т. н. квантовую криптографию. Это одно из фантастических применений, которое стало возможным благодаря лазерам и законам квантовой механики.

Квантовая криптография является новым методом засекречивания передачи информации. В отличие от обычных методов криптографии, в квантовой криптографии зашифровка передаваемой информации осуществляется благодаря законам физики. Криптография имеет долгую и замечательную историю в военном деле и в дипломатии, со времен античной Греции. В настоящее время секретность информации становится очень важной и для коммерческой деятельности. В добавок к практическим возможным применениям, квантовая криптография иллюстрирует несколько интересных аспектов квантовой оптики, включая роль принципа неопределенности Гейзенберга в оптических измерениях и двухфотонной интерферометрии.

Первые методы криптографии использовали секретный код (ключ) для зашифровки послания перед его отправкой и для расшифровки при получении. Секретность этих методов часто оказывается под угрозой из-за похищения кода, или анализа, который приводит к расшифровке кода, или ошибок, т.е. всего, что ломает код. Самые современные методы не используют секретный код, а основаны на математических изощренных методах, с помощью которых раскрытие содержания послания представляет результат поиска всех возможных комбинаций, чтобы найти правильную. В любом случае секретность этих методов может быть взломана неожиданными успехами математических технологий расшифровки или увеличения быстродействия компьютеров.

Квантовая криптография использует секретный ключ для кодирования и декодирования информации, которая передается по открытым каналам, но сам ключ не передается обычным способом. Один из методов квантовой криптографии устанавливает идентичные ключи в двух разных местах без передачи какой-либо информации. Хотя это может показаться невозможным с точки зрения классической физики, это становится возможным благодаря нелокальным свойствам двухфотонного интерферометра. В другом методе, с другой стороны, ключ посылается в форме одиночных фотонов, а принцип неопределенности квантовой механики обеспечивает невозможность несанкционированного перехвата информации.

Все методы квантовой криптографии основаны на принципе, что в квантовой механике любое измерение возмущает систему непредсказуемым образом. Объяснить в деталях, как это удивительное применение работает, не легко. Мы ограничимся представлением некоторых идей случая, в котором используется т.н. метод двухфотонной интерферометрии.

Рассмотрим рис. 67. Два человека, Алиса и Боб, находятся на большом расстоянии друг от друга, и имеют два одинаковых интерферометра, в которых используются два полностью отражающих и два частично отражающих зеркала, как показано на рис. 67. Один фотон, который приходит на один из двух интерферометров, например на левый, имеет, согласно квантовой механике, две возможности: либо прямо распространяться от S’ 1до S’ 2либо, следуя путем S’ 1, S’ 2, S’ 3, S’4. Если эти два пути очень отличаются друг от друга, то интерференция не происходит, и поэтому в первом случае фотон идет в направлении 24, в то время как во втором он идет в направлении 2В. То же самое происходит и для фотона, который попадает на другой интерферометр. Возможные результаты A и B обозначены, как 1A и 1B для правого интерферометра, и 2A и 2B для левого интерферометра, чтобы различать их.

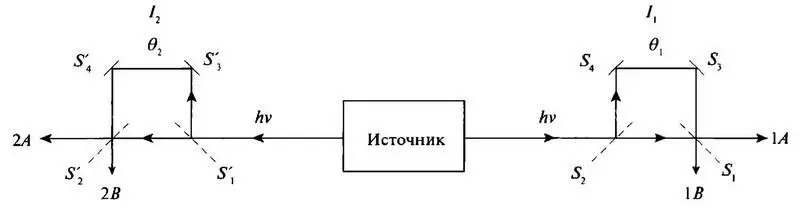
Рис. 67. Метод двухфотонной интерферометрии. Два интерферометра I 1и I 2включают четыре зеркала S 4, S 3, S’ 4, S’ 3(полностью отражаемых) и четыре зеркала S 1, S 2, S’ 1, S’ 2(полупрозрачных). Выходы 1А и 2А представляют, например, бит 0, тогда как выходы 1В и 2B представляют бит 1

Теперь главный момент! Одной из возможностей нелинейной оптики является получение новых цветов света, которые получаются из-за того, что в нелинейном материале два фотона, имеющие некоторые частоты, т.е. некоторые энергии, сливаются в один фотон, энергия которого является суммой двух фотонов, и поэтому его частота является суммой двух частот. Если оба фотона имеют одну и ту же частоту, тогда новый фотон имеет удвоенную частоту. Это явление известно как генерация второй гармоники. Если два фотона имеют разные частоты, тогда говорят о параметрическом эффекте. Также возможно получить другой, обратный, процесс, в котором фотон при нелинейном взаимодействии распадается на два фотона, каждый из которых, имеет частоту, в точности равной половине частоты первоначального фотона. Этот процесс называют даун-конверсией. Законы этого процесса гарантируют, что оба фотона испускаются в одно и то же время, несмотря даже на то, что квантовая механика (принцип неопределенности) не допускает знание точного момента, когда они испускаются, так как их энергии точно известны.