Позвольте пояснить одну неточность. Из уравнения Шрёдингера следует, что значения, которые может принимать квантовая волна (или, на языке полей, волновая функция) могут быть положительными и отрицательными; в общем случае, эти значения могут быть комплексными числами. Такие числа не могут быть напрямую интерпретированы как вероятности — что означает отрицательная или комплексная вероятности? Вероятности ассоциируются с квадратом амплитуды квантовой волны в данной точке. Математически это означает, что для определения вероятности нахождения частицы в данной точке мы перемножаем значение волны в этой точке с его комплексно сопряжённым значением . Это пояснение также важно для понимания следующего вопроса. Сокращения между перекрывающимися волнами необходимы для появления интерференционной картины. Но если бы волны действительно описывались как волны вероятности, такие сокращения не происходили бы, потому что вероятности являются положительными числами. Однако, как мы теперь знаем, квантовые волны принимают не только положительные значения; благодаря этому и происходят сокращения между положительными и отрицательными числами, а в общем случае, между комплексными числами. Поскольку нам важны только качественные свойства таких волн, для упрощения обсуждения в основном тексте я не буду различать квантовые волны и связанные с ними волны вероятности (получаемые путём возведением амплитуды в квадрат).
Для математически подготовленного читателя заметим, что квантовая волна ( волновая функция ) одной частицы с большой массой будет описываться так, как это указано в основном тексте. Однако очень массивные объекты, как правило, состоят из многих частиц. В такой ситуации квантово-механическое описание более сложное. Вы могли бы подумать, что все частицы будут описываться квантовой волной, определённой на той же сетке координат, которая использовалась для одной частицы — с помощью тех же трёх пространственных осей. Но это не так. Волна вероятности использует в качестве начальных данных возможное положение каждой частицы и задаёт вероятность нахождения частиц в этих положениях. Следовательно, волна вероятности живёт в пространстве с тремя осями для каждой из частиц — то есть общее количество осей будет в три раза больше количества частиц (или в десять раз больше количества частиц, если учитывать дополнительные измерения теории струн). Это означает, что волновая функция составной системы, состоящей из n фундаментальных частиц, будет являться комплекснозначной функцией, определённой не на обычном трёхмерном пространстве, а на 3 n -мерном пространстве; если число пространственных измерений не 3, а m , то число 3 в этом выражении будет заменено на m . Такое пространство называется конфигурационным . То есть в общем случае, волновая функция будет отображением 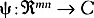 . Когда мы говорим, что волновая функция имеет острый пик, мы имеем в виду, что это отображение определено на небольшом mn -мерном шаре внутри области определения. Отметим, в частности, что волновая функция, как правило, определена не в привычном пространстве. Конфигурационное пространство совпадает с привычным нам пространством только в идеализированном случае волновой функции одной, полностью изолированной, частицы. Ещё заметим, что когда говорится, что квантовые законы гарантируют распространение остролокализованной волновой функции массивного объекта по траектории, которую задают уравнения Ньютона, можно представлять себе, что волновая функция описывает движение центра масс данного объекта.
. Когда мы говорим, что волновая функция имеет острый пик, мы имеем в виду, что это отображение определено на небольшом mn -мерном шаре внутри области определения. Отметим, в частности, что волновая функция, как правило, определена не в привычном пространстве. Конфигурационное пространство совпадает с привычным нам пространством только в идеализированном случае волновой функции одной, полностью изолированной, частицы. Ещё заметим, что когда говорится, что квантовые законы гарантируют распространение остролокализованной волновой функции массивного объекта по траектории, которую задают уравнения Ньютона, можно представлять себе, что волновая функция описывает движение центра масс данного объекта.
Из этого описания вы можете сделать вывод, что существует бесконечно много местоположений, где может находиться электрон: для заполнения плавно меняющегося волнового профиля квантовой волны понадобится бесконечное число пикообразных форм, каждая из которых ассоциирована с возможным положением электрона. Как это стыкуется с главой 2, в которой мы обсуждали конечное число различных конфигураций частиц? Во избежание постоянных оговорок, не имеющих важного значения для основного изложения этой книги, я не стал заострять внимание на факте (указанном в главе 2), что для всё более точного определения положения электрона измерительный прибор будет тратить всё больше энергии. Поскольку в реальных ситуациях энергия ограничена, то разрешение прибора не идеально. Для пикообразных квантовых волн это означает, что при любой конечной энергии у пиков имеется отличная от нуля ширина. В свою очередь это означает, что в любой ограниченной области (например, внутри космического горизонта) существует конечное число различных измеряемых положений электрона. Более того, чем тоньше пик (более точное разрешение положения частицы), тем шире квантовая волна, описывающая энергию частиц, что демонстрирует обусловленный принципом неопределённости компромисс между характеристиками частицы.
Читать дальше

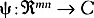 . Когда мы говорим, что волновая функция имеет острый пик, мы имеем в виду, что это отображение определено на небольшом mn -мерном шаре внутри области определения. Отметим, в частности, что волновая функция, как правило, определена не в привычном пространстве. Конфигурационное пространство совпадает с привычным нам пространством только в идеализированном случае волновой функции одной, полностью изолированной, частицы. Ещё заметим, что когда говорится, что квантовые законы гарантируют распространение остролокализованной волновой функции массивного объекта по траектории, которую задают уравнения Ньютона, можно представлять себе, что волновая функция описывает движение центра масс данного объекта.
. Когда мы говорим, что волновая функция имеет острый пик, мы имеем в виду, что это отображение определено на небольшом mn -мерном шаре внутри области определения. Отметим, в частности, что волновая функция, как правило, определена не в привычном пространстве. Конфигурационное пространство совпадает с привычным нам пространством только в идеализированном случае волновой функции одной, полностью изолированной, частицы. Ещё заметим, что когда говорится, что квантовые законы гарантируют распространение остролокализованной волновой функции массивного объекта по траектории, которую задают уравнения Ньютона, можно представлять себе, что волновая функция описывает движение центра масс данного объекта.










