Для читателя с философским складом ума замечу, что описанная выше двухъярусная картина научного объяснения была предметом философских обсуждений и споров. Смежные идеи и обсуждения можно найти в работах: Frederick Suppe, «The Semantic Conception of Theories and Scientific Realism». Chicago: University of Illinois Press, 1989; James Ladyman, Don Ross, David Spurrett, & John Collier, «Every Thing Must Go». Oxford: Oxford University Press, 2007.
Физики часто довольно свободно говорят о бесконечном количестве вселенных в контексте многомирового подхода к квантовой механике. Безусловно, существует бесконечно много форм возможных волн вероятности. Даже в одной и той же точке пространства можно непрерывным образом изменять значение волны вероятности, и поэтому число принимаемых ею значений будет бесконечным. Однако волны вероятности не являются физическими характеристиками системы, к которым у нас есть прямой доступ. Наоборот, волны вероятности содержат информацию о возможных различных исходах в заданной ситуации, а их не обязательно бесконечное число. В частности, подготовленный читатель заметит, что квантовая волна (волновая функция) находится в гильбертовом пространстве. Если данное гильбертово пространство конечномерно, то имеется конечное число разных возможных результатов измерений в физической системе, задаваемой этой волновой функцией (то есть любой эрмитов оператор имеет конечное число различных собственных значений). Это приведёт к конечному числу миров для конечного числа наблюдений или измерений. Считается, что гильбертово пространство, ассоциированное с физическими явлениями, происходящими внутри пространства конечного объёма и с ограниченной энергией, является с необходимостью конечномерным (мы остановимся на этом более подробно в главе 9), откуда следует, что число миров также будет конечно.
См.: Peter Byrne, «The Many Worlds of Hugh Everett III». New York: Oxford University Press, 2010, p. 177.
В разное время многие учёные, включая Нила Грахама; Брайса де Витта; Джеймса Хартли; Эварда Фархи, Джефри Голдстоуна и Сэма Гутмана; Дэвида Дойча; Сидни Коулмена; Дэвида Альберта и других, включая меня самого, независимо обнаружили удивительный математический факт, который, по видимому, является центральным для понимания природы вероятности в квантовой механике. Приведём его формулировку для математически подготовленного читателя: пусть ψ — волновая функция квантово-механической системы — вектор, являющийся элементом гильбертова пространства H . Волновая функция для n тождественных копий системы имеет, таким образом, вид 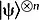 . Пусть A — это произвольный эрмитов оператор с собственными значениями α k и собственными функциями
. Пусть A — это произвольный эрмитов оператор с собственными значениями α k и собственными функциями 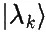 . Пусть F K ( A ) — это оператор «частоты», который подсчитывает число раз, которое
. Пусть F K ( A ) — это оператор «частоты», который подсчитывает число раз, которое 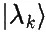 появляется в данном состоянии, принадлежащем
появляется в данном состоянии, принадлежащем 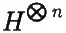 . Тогда имеем следующий математический результат:
. Тогда имеем следующий математический результат:
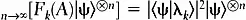
То есть при неограниченном росте числа тождественных копий системы волновая функция всей составной системы стремится к собственной функции оператора частоты с собственным значением 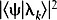 . Это замечательный результат. Из самого определения собственной функции тогда следует, что в указанном пределе наблюдатель, измеряющий A , обнаружит α k дробное число раз, равное
. Это замечательный результат. Из самого определения собственной функции тогда следует, что в указанном пределе наблюдатель, измеряющий A , обнаружит α k дробное число раз, равное 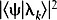 , что выглядит как самый прямой вывод знаменитого правила Борна для квантово-механической вероятности. С точки зрения многомирового подхода это означает, что миры, в которых число наблюдений α k не согласуется с правилом Борна, обладают нулевой нормой в гильбертовом пространстве в пределе произвольно больших n . В этом смысле кажется, будто квантово-механическая вероятность имеет прямую интерпретацию в рамках многомирового подхода. Все наблюдатели в многомировом подходе будут видеть результаты с частотами, которые соответствуют возникающим из стандартной квантовой механики, за исключением множества наблюдателей, норма которых в гильбертовом пространстве становится исчезающее мала при n , стремящемся к бесконечности. Хотя это выглядит многообещающим, но по зрелому размышлению возникают сомнения. В каком смысле можно говорить, что наблюдатель, норма которого в гильбертовом пространстве мала или норма которого стремится к нулю при n , стремящемся к бесконечности, неважен или не существует? Мы хотим сказать, что такие наблюдатели аномальны или «маловероятны», но как установить связь между нормой вектора в гильбертовом пространстве и этими характеристиками? Ситуацию можно разъяснить на примере. В двумерном гильбертовом пространстве с состояниями спин-вверх
, что выглядит как самый прямой вывод знаменитого правила Борна для квантово-механической вероятности. С точки зрения многомирового подхода это означает, что миры, в которых число наблюдений α k не согласуется с правилом Борна, обладают нулевой нормой в гильбертовом пространстве в пределе произвольно больших n . В этом смысле кажется, будто квантово-механическая вероятность имеет прямую интерпретацию в рамках многомирового подхода. Все наблюдатели в многомировом подходе будут видеть результаты с частотами, которые соответствуют возникающим из стандартной квантовой механики, за исключением множества наблюдателей, норма которых в гильбертовом пространстве становится исчезающее мала при n , стремящемся к бесконечности. Хотя это выглядит многообещающим, но по зрелому размышлению возникают сомнения. В каком смысле можно говорить, что наблюдатель, норма которого в гильбертовом пространстве мала или норма которого стремится к нулю при n , стремящемся к бесконечности, неважен или не существует? Мы хотим сказать, что такие наблюдатели аномальны или «маловероятны», но как установить связь между нормой вектора в гильбертовом пространстве и этими характеристиками? Ситуацию можно разъяснить на примере. В двумерном гильбертовом пространстве с состояниями спин-вверх 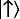 и спин-вниз
и спин-вниз 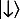 рассмотрим состояние
рассмотрим состояние 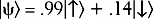 . При измерении это состояние даёт вероятность состояния спин-вверх примерно 0,98 и состояния спин-вниз примерно 0,02. Если рассмотреть n копий этой спиновой системы,
. При измерении это состояние даёт вероятность состояния спин-вверх примерно 0,98 и состояния спин-вниз примерно 0,02. Если рассмотреть n копий этой спиновой системы,  , то при стремлении n к бесконечности подавляющее большинство членов в разложении этого вектора имеют примерно одинаковые количества состояний спин-вверх и спин-вниз. Поэтому подавляющее большинство наблюдателей (копий экспериментаторов) будут видеть состояния спин-вверх и спин-вниз в отношении, которое не согласуется с квантово-механическими предсказаниями. Лишь небольшое количество членов в разложении
, то при стремлении n к бесконечности подавляющее большинство членов в разложении этого вектора имеют примерно одинаковые количества состояний спин-вверх и спин-вниз. Поэтому подавляющее большинство наблюдателей (копий экспериментаторов) будут видеть состояния спин-вверх и спин-вниз в отношении, которое не согласуется с квантово-механическими предсказаниями. Лишь небольшое количество членов в разложении  , у которых 98 процентов состояний спин-вверх и 2 процента состояний спин-вниз, будут согласованы с квантово-механическим ожиданием. Этот результат говорит нам, что только эти состояния и будут теми единственными, имеющими ненулевую норму при n , стремящемся к бесконечности. Тогда абсолютное большинство членов в разложении
, у которых 98 процентов состояний спин-вверх и 2 процента состояний спин-вниз, будут согласованы с квантово-механическим ожиданием. Этот результат говорит нам, что только эти состояния и будут теми единственными, имеющими ненулевую норму при n , стремящемся к бесконечности. Тогда абсолютное большинство членов в разложении  (абсолютное большинство копий экспериментаторов) следует рассматривать в некотором смысле как «несуществующие». Проблема состоит в том, чтобы понять, что всё это вообще значит.
(абсолютное большинство копий экспериментаторов) следует рассматривать в некотором смысле как «несуществующие». Проблема состоит в том, чтобы понять, что всё это вообще значит.
Читать дальше

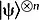 . Пусть A — это произвольный эрмитов оператор с собственными значениями α k и собственными функциями
. Пусть A — это произвольный эрмитов оператор с собственными значениями α k и собственными функциями 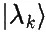 . Пусть F K ( A ) — это оператор «частоты», который подсчитывает число раз, которое
. Пусть F K ( A ) — это оператор «частоты», который подсчитывает число раз, которое 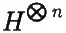 . Тогда имеем следующий математический результат:
. Тогда имеем следующий математический результат: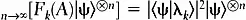
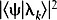 . Это замечательный результат. Из самого определения собственной функции тогда следует, что в указанном пределе наблюдатель, измеряющий A , обнаружит α k дробное число раз, равное
. Это замечательный результат. Из самого определения собственной функции тогда следует, что в указанном пределе наблюдатель, измеряющий A , обнаружит α k дробное число раз, равное 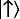 и спин-вниз
и спин-вниз 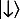 рассмотрим состояние
рассмотрим состояние 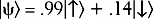 . При измерении это состояние даёт вероятность состояния спин-вверх примерно 0,98 и состояния спин-вниз примерно 0,02. Если рассмотреть n копий этой спиновой системы,
. При измерении это состояние даёт вероятность состояния спин-вверх примерно 0,98 и состояния спин-вниз примерно 0,02. Если рассмотреть n копий этой спиновой системы,  , то при стремлении n к бесконечности подавляющее большинство членов в разложении этого вектора имеют примерно одинаковые количества состояний спин-вверх и спин-вниз. Поэтому подавляющее большинство наблюдателей (копий экспериментаторов) будут видеть состояния спин-вверх и спин-вниз в отношении, которое не согласуется с квантово-механическими предсказаниями. Лишь небольшое количество членов в разложении
, то при стремлении n к бесконечности подавляющее большинство членов в разложении этого вектора имеют примерно одинаковые количества состояний спин-вверх и спин-вниз. Поэтому подавляющее большинство наблюдателей (копий экспериментаторов) будут видеть состояния спин-вверх и спин-вниз в отношении, которое не согласуется с квантово-механическими предсказаниями. Лишь небольшое количество членов в разложении 










