Брайан Грин - Скрытая реальность. Параллельные миры и глубинные законы космоса

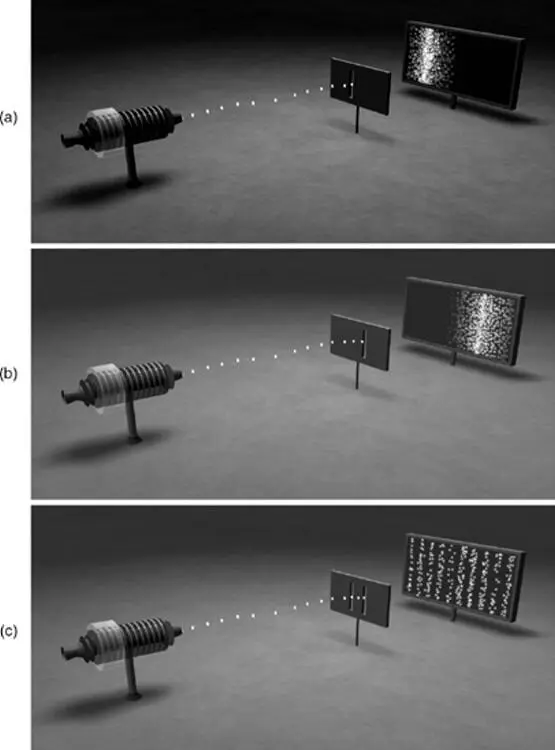
Рис. 8.2. а ) Открыта только левая щель; б ) Открыта только правая щель; в ) Открыты обе щели

Этот результат отличается от ожидаемого самым странным образом. Тёмные полосы соответствуют местам обильного попадания электронов, когда открыта только правая или только левая щель ( яркие области на рис. 8.2 а и 8.2 б ), но они, оказывается, исчезают, когда открыты две щели. Таким образом, наличие левой щели изменяет возможные места попадания электронов, прошедших через правую щель, и наоборот. Это совершенно сбивает с толку. Для таких крохотных частиц, как электрон, расстояние между щелями огромно. Поэтому когда электрон проходит сквозь одну из щелей, то каким образом наличие или отсутствие другой щели может привести к хоть какому-то эффекту, не говоря уже о наблюдаемой поразительной картинке? Это похоже на то, как если бы вы в течение многих лет успешно заходили в здание, где работаете, через одну дверь, а когда руководство, наконец, решило сделать ещё один вход с другой стороны здания, то вы не смогли бы попасть в свой кабинет!

Как это понять? Эксперимент с двумя щелями неизбежно приводит к заключению, которое трудно осознать. Независимо от того, через какую щель прошёл электрон, он каким-то образом «знает» о существовании другой щели. Есть что-то, связанное с электроном, или сопоставляемое с ним, или являющееся его частью, на что влияют сразу две щели.

Что бы это могло быть?

Как можно объяснить, что электрон, проходящий сквозь одну щель, «знает» о другой? В качестве подсказки рассмотрим более подробно картинку, показанную на рис. 8.2 в . Эта картинка с чередующимися полосами по типу «светлая — темноватая — тёмная» хорошо знакома любому физику. Она говорит нам — нет, она кричит — волны ! Если вы когда-нибудь бросали в воду два камешка и потом наблюдали, как возникающие волны разбегаются и накладываются друг на друга, вы поймёте, что я имею в виду. Там, где гребень одной волны накладывается на гребень другой, результирующая волна высока; там, где впадина одной волны совпадает со впадиной другой волны, также впадина и у результирующей волны; но самое главное происходит, когда гребень одной волны пересекается со впадиной другой волны — тогда волны гасят друг друга и поверхность воды остаётся гладкой. Всё это проиллюстрировано на рис. 8.3. Если бы мы положили экран детектора на картинку, на которой отражён уровень волнения в каждой точке — чем сильнее волнение, тем ярче, — то результат предстал бы на экране в виде чередующихся ярких и тёмных областей. Там, где волны усиливают друг друга, что приводит к повышению уровня воды, находятся яркие области; тёмные области соответствуют самому низкому уровню воды там, где волны гасят друг друга. Физики говорят, что накладывающиеся волны интерферируют друг с другом, и называют чередование тёмных и светлых полос интерференционной картиной .

Рис. 8.3.Когда две волны на поверхности воды накладываются, они «интерферируют», образуя чередование областей с бо́льшим и меньшим волнением, что называется интерференционной картиной

Сходство с рис. 8.2 в совершенно очевидно, поэтому глядя на данные по рассеянию электронов, мы начинаем думать о волнах. Хорошо. Это уже кое-что. Но детали происходящего по-прежнему остаются неясными. Что за волны? Откуда они? И как они связаны с частицами, такими как электроны?

Следующую подсказку даёт эксперимент, о котором я упомянул вначале. Собранные данные о движении частиц показывают, что полученные закономерности носят исключительно статистический характер. Проведя точно такие же измерения над идентично приготовленными частицами, мы увидим, что частицы, вообще говоря, окажутся в других местах; однако проведя большое количество таких измерений, мы обнаружим, что частицы в среднем обладают одинаковой вероятностью оказаться в любом заданном месте. В 1926 году немецкий физик Макс Борн, собрав воедино эти две подсказки, выдвинул неожиданную идею, которая спустя почти три десятилетия привела его к Нобелевской премии. Итак, есть экспериментальное подтверждение, что волны здесь как-то при чём. Есть экспериментальное подтверждение, что и вероятность здесь как-то при чём. Возможно, предположил Борн, волна, связанная с частицей, является волной вероятности .