Брайан Грин - Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)

Червоточина создает новое пространство и потому прокладывает новую пространственную территорию. Существуют ли червоточины во Вселенной? Этого не знает никто. И если они действительно существуют, неясно, могут ли они быть только микроскопической формы, или перекрывать обширные области пространства, как в фантастических фильмах. Существование червоточин в реальном мире во многом определяется тем, возможен ли разрыв структуры пространства.

Другой яркий пример того, как ткань пространства может растягиваться до предела, дают черные дыры. На примере рис. 3.7 мы видели, что сильнейшее гравитационное поле черной дыры приводит к настолько сильной искривленности пространства, что оно выглядит проколотым в центре черной дыры. В отличие от червоточин, есть веские экспериментальные свидетельства в пользу существования черных дыр, и вопрос о том, что происходит в центре дыры, приобретает конкретный научный характер. В экстремальных условиях внутри черной дыры уравнения общей теории относительности становятся неприменимыми. По мнению некоторых физиков, в центре черной дыры действительно имеется прокол, но мы ограждены от этой космической «сингулярности» горизонтом событий, не позволяющим даже свету вырваться из гравитационной ловушки. Такие соображения привели Роджера Пенроуза из Оксфордского университета к «гипотезе космической цензуры», согласно которой подобные пространственные особенности возможны лишь в местах, тщательно скрытых от наших глаз пеленой горизонта событий. С другой стороны, до открытия теории струн некоторые физики считали, что корректное объединение квантовой теории и общей теории относительности «залатает» бросающиеся в глаза бреши в ткани пространства, сгладив его квантовыми поправками.

С открытием теории струн, органично связывающей квантовую теорию с гравитацией, появилась твердая почва для исследования этих вопросов. На сегодняшний день они окончательно не решены, но в последние годы были решены тесно связанные с ними вопросы. В этой главе мы покажем, что в теории струн впервые явно демонстрируется возможность разрыва ткани пространства при определенных физических явлениях (в некоторых отношениях отличных от явлений пространственных червоточин и черных дыр).

В 1987 г. Шин-Тун Яу и его студент Ганг Тиан, работающий сейчас в Массачусетсом технологическом институте, сделали интересное математическое наблюдение. Используя хорошо известный математический прием, они обнаружили, что одни многообразия Калаби-Яу можно преобразовать в другие путем протыкания их поверхности и сшивания образовавшегося отверстия согласно строго определенной математической процедуре2). Грубо говоря, они обнаружили, что внутри исходного пространства Калаби-Яу можно выделить двумерную сферу определенного вида (рис. 11.2). (Двумерная сфера аналогична поверхности надувного мяча, который, как и все знакомые нам объекты, трехмерен. Здесь, однако, мы говорим только о поверхности, не учитывая толщину материала, из которого сделан мяч, а также пространство внутри него. Точки на поверхности мяча определяются двумя числами, «широтой» и «долготой», аналогично тому, как определяются координаты на поверхности Земли. Вот почему поверхность мяча, как и поверхность упоминавшегося в предыдущих главах Садового шланга, является двумерной.)

Рис. 11.2. В выделенной области внутри пространства Калаби-Яу находится сфера.

Далее они рассмотрели стягивание сферы в одну точку; этот процесс показан на рис. 11.3. Как и все последующие рисунки этой главы, он упрощен с целью наглядности изображения наиболее важного «куска» пространства Калаби-Яу: но вы должны помнить, что такие преобразования происходят внутри несколько большего пространства Калаби-Яу, подобного изображенному на рис. 11.2.

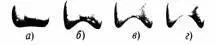
Рис. 11.3. Сфера внутри пространства Калаби-Яу. сжимается в точку, приводя к перетяжке в ткани пространства. На этом и следующих рисунках для простоты показана лишь часть всего пространства Калаби-Яу

И, наконец, Тиан и Яу рассмотрели случай, когда в точке сжатия пространство Калаби-Яу слегка надрывается (рис. 11.4 а), раскрывается и перестраивается в другую шарообразную фигуру (рис. 11.4 б), которую затем снова можно раздуть до нормального размера (рис. 11.4 в и 11.4 г).