If Miller’s planet is, indeed, close enough to Gargantua to experience extreme time slowing—as I chose for my interpretation of the movie—then it must be deep into the cylindrical region of Gargantua’s warped space, as depicted in Figure 17.1. It seems likely, then, that if you look down the cylinder from Miller’s planet you will see Gargantua, and if you look up the cylinder you will see the external universe; so Gargantua should encompass roughly half of the sky (180 degrees) around the planet and the universe the other half. Indeed, that is what Einstein’s relativistic laws predict.
It also seems clear that, since Miller’s planet is the closest anything can live stably, without falling into Gargantua, the entire accretion disk should be outside the orbit of Miller’s planet. Therefore, as the crew approach the planet, they should see a giant disk above them and a giant black-hole shadow below. Again, that is what Einstein’s laws predict.
If Chris had followed these dictates of Einstein’s laws, it would have spoiled his movie. To see such fantastic sights so early in the movie would make the movie’s climax, when Cooper falls into Gargantua, visually anticlimactic. So Chris consciously saved such sights for the end of the movie; and invoking artistic license, near Miller’s planet he depicted Gargantua and its disk together, “just” twenty times bigger than the Moon looks from Earth.

Fig. 17.9. Gargantua and its disk, partially eclipsed by Miller’s planet, as the Ranger, in the foreground, descends toward landing. [From Interstellar , used courtesy of Warner Bros. Entertainment Inc.]
Although I’m a scientist and aspire to science accuracy in science fiction, I can’t blame Chris at all. I would have done the same, had I been making the decision. And you’d have thanked me for it.
18
Gargantua’s Vibrations

While Cooper and Amelia Brand are on Miller’s planet, Romilly stays behind in the Endurance , observing Gargantua. From exquisitely accurate observations, he hopes to learn more about gravitational anomalies. Above all (I presume), he hopes that quantum data from Gargantua’s singularity (Chapter 26) will leak out through the event horizon, bringing information about how to control the gravitational anomalies (Chapter 24). Or, in Romilly’s pithy language, bringing information for “solving gravity.”
When Amelia Brand returns from Miller’s planet, Romilly tells her, “I learned what I could from studying the black hole, but I couldn’t send anything to your father. We’ve been receiving but nothing gets out.”
What did Romilly observe? He’s not specific, but I presume he would focus on Gargantua’s vibrations, and I offer this chapter’s extrapolation of the movie for that.
Vibrations of Black Holes
In 1971 Bill Press, a student of mine at Caltech, discovered that black holes can vibrate at special, resonant frequencies , in much the same way as a violin string vibrates.
When a violin string is plucked just right, it emits a very pure tone: sound waves with a single frequency. When plucked a little differently, it emits that pure tone and also higher harmonics of the pure tone. In other words (if the string is firmly clamped, with the clamping finger not moving around) its vibrations produce sound at only a discrete set of frequencies, the string’s resonant frequencies.
The same is true of a wine glass whose rim you rub with your finger, and a bell struck by a hammer. And also a black hole disturbed by something falling into it, Press discovered.
A year later Saul Teukolsky, another of my students, used Einstein’s relativistic laws to work out a mathematical description of these resonant vibrations for a spinning black hole. (That’s the best thing about teaching at Caltech; we get fabulous students!) By solving Teukolsky’s equations, we physicists can compute a black hole’s resonant frequencies. But solving them for an extremely fast spinning hole (like Gargantua) is very difficult. So difficult that it was not done successfully until forty years later—by a collaboration in which the lead players again were two Caltech students: Huan Yang and Aaron Zimmerman.
In September 2013, Ritchie Kremer, the property master for Interstellar (the person in charge of props) asked me for observational data that Romilly could show to Brand. Of course, I turned to the world’s best experts for help: Yang and Zimmerman. They quickly produced tables of Gargantua’s resonant vibration frequencies and also of the rates that the vibrations die out by feeding energy into gravitational waves—tables based on their own calculations using Teukolsky’s equations. Then they added fake observational numbers to go along with the theoretical predictions and I added pictures of Gargantua’s event horizon (or rather, the edge of its shadow), pictures from simulations by the Interstellar visual-effects team at Double Negative . The result was Romilly’s observational data set.
When Christopher Nolan filmed the scene where Romilly discusses his observations with Amelia Brand, Romilly wound up not actually showing her his data set. It was there on a table, but he didn’t pick it up. However, the data set is central to my science extrapolation of Interstellar .
Gargantua’s Resonant Vibrations
Figure 18.1 is the data set’s first page. Each line of data on that page refers to a single resonant frequency at which Gargantua vibrates.
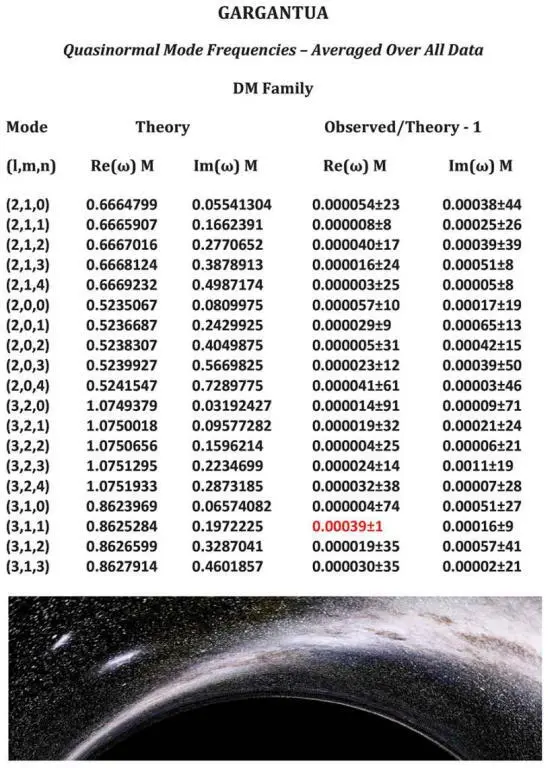
Fig. 18.1. The first page of the data that Yang and Zimmermann prepared for Romilly to show to Amelia Brand. [Prop from Interstellar , used courtesy of Warner Bros. Entertainment Inc.]
The first column is a three-number code for the shape of Gargantua’s vibrations and the picture is a still from a movie Romilly took, in my extrapolation of Interstellar , which verified that the vibrations had the predicted shape. The second column of data is the vibration frequency and the third is the rate at which this vibration dies out, as predicted by Teukolsky’s equations. [32] The table’s numerical values for the resonant frequencies are not in familiar units. To convert to familiar units, we must multiply by the cube of the speed of light and divide by 2π GM , where π = 3.14159…, G is Newton’s gravitational constant, and M is Gargantua’s mass. This conversion factor is approximately one vibration per hour, so the first predicted frequency in the table is about 0.67 vibrations per hour. The conversion factor for the die-out rate is the same.
The fourth and fifth columns show the difference between Romilly’s observations and the theoretical predictions.
In my extrapolation Romilly finds a few anomalies, severe disagreements between his observations and the theory. He prints the disagreements in red. On page one of the data set (Figure 18.1), there is just one anomaly, but the disagreement is severe: thirty-nine times larger than the uncertainty in his measurements!
These anomalies might be helpful in “solving gravity” (learning how to harness the anomalies), Romilly thinks, in my extrapolation. He wishes he could transmit what he has learned to Professor Brand back on Earth, but the outbound communication link has been severed, so he’s frustrated.
Читать дальше















