With further lengthening (bottom picture), the primary image shrinks further, all the images move inward, a fourth image emerges from the left edge of the crystal ball, a fifth from the right, and so forth.
These behaviors can be understood by drawing light rays on the wormhole as seen from the bulk (Figure 15.3). The primary image is carried by the black light ray (1), which travels on the shortest possible path from Saturn to the camera, and by a bundle of rays tightly surrounding it. The secondary image is carried by a bundle surrounding the red ray (2), which travels around the wormhole’s wall in the opposite direction to the black ray: counterclockwise. This red ray is the shortest possible counterclockwise ray from Saturn to the camera. The tertiary image is carried by a bundle surrounding the green ray (3), which is the shortest possible clockwise ray that makes more than one full trip around the wormhole. And the fourth image is carried by a bundle surrounding the brown ray (4): the shortest possible counterclockwise ray that makes more than one full trip around the wormhole.
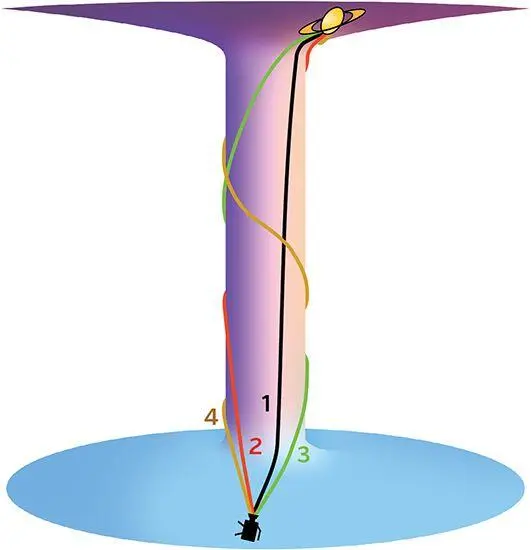
Fig. 15.3. Light rays from Saturn, through the wormhole, to the camera.
Can you explain the fifth and sixth images? and explain why the images shrink when the wormhole is lengthened? and explain why the images appear to emerge from the edge of the wormhole’s crystal-ball mouth and move inward?
The Wormhole’s Lensing Width
Having understood how the wormhole’s length affects what the camera sees, we then fixed the length to be fairly short, the same as the wormhole’s radius, and varied the gravitational lensing. We increased the wormhole’s lensing width from near zero to about half the wormhole’s diameter and computed what that did to the images the camera sees. Figure 15.4 shows the two extremes.
With very small lensing width, the wormhole shape (upper left) has a sharp transition from the external universe (horizontal sheets) to the wormhole throat (vertical cylinder). As seen by the camera (upper right), the wormhole distorts the star field and a dark cloud in the upper left only slightly, near the wormhole’s edge. Otherwise it simply masks the star field out, as would any opaque body with weak gravity, for example a planet or a spacecraft.
In the lower half of Figure 15.4, the lensing width is about half the wormhole’s radius, so there is a slow transition from the throat (vertical cylinder) to the external universe (asymptotically horizontal sheet).
With this large lensing width, the wormhole strongly distorts the star field and dark cloud (lower right in Figure 15.3) in nearly the same way as does a nonspinning black hole (Figures 8.3 and 8.4), producing multiple images. And the lensing also enlarges the secondary and tertiary images of Saturn. The wormhole looks bigger in the lower half of Figure 15.3 than in the upper half. It subtends a larger angle as seen by the camera. This is not because the camera is closer to the mouth; it is not closer. The camera is the same distance in both pictures. The enlargement is entirely due to the gravitational lensing.
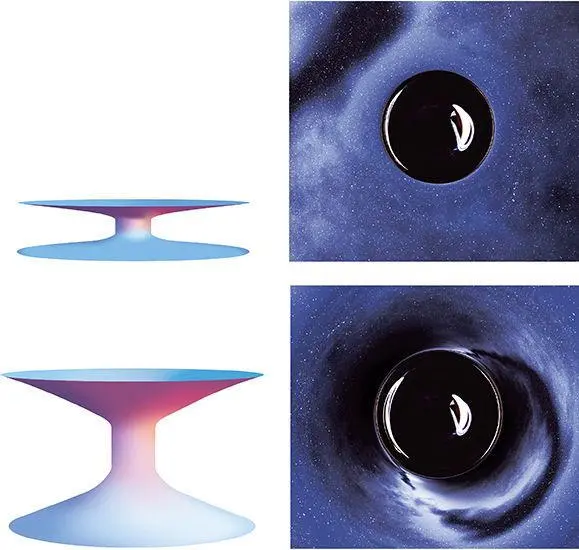
Fig. 15.4. Wormhole’s gravitational lensing of a star field and Saturn: influence of the lensing width which is 0.014 and 0.43 times the wormhole radius in the top and bottom images. [From simulations by Eugénie von Tunzelmann’s team using Oliver James’ code based on my equations.]
When Chris saw the various possibilities, with varying wormhole length and lensing width, his choice was unequivocal. For medium and large length the multiple images seen through the wormhole would be confusing to a mass audience, so he made Interstellar ’s wormhole very short: 1 percent of the wormhole radius. And he gave Interstellar ’s wormhole a modest lensing width, about 5 percent of the wormhole radius, so the lensing of stars around it would be noticeable and intriguing, but much smaller than Gargantua’s lensing.
The resulting wormhole is the one at the top of Figure 15.2. And in Interstellar , after the Double Negative team had created for its far side a galaxy with beautiful nebulae, dust lanes, and star fields, it is marvelous to behold (Figure 15.5). To me it is one of the movie’s grandest sights.

Fig. 15.5. The wormhole as seen in a trailer for Interstellar . The Endurance is in front of the wormhole, near the center. Around the wormhole in pink I have drawn the Einstein ring, like that in Figure 8.4 for a nonspinning black hole. Primary and secondary images of gravitationally lensed stars move in the same way here as there. Looking at the trailer, can you identify some and trace their motion? [From Interstellar , used courtesy of Warner Bros. Entertainment Inc.]
The Trip Through the Wormhole
On April 10, 2014, I got an urgent phone call. Chris was having trouble with visualizing the Endurance ’s trip through the wormhole and he wanted advice. I drove over to his Syncopy compound where postproduction editing was underway, and Chris showed me the problem.
Using my equations, Paul’s team had produced visualizations for wormhole trips with various wormhole lengths and lensing widths. For the short, modest-lensing wormhole depicted in the movie, the trip was quick and uninteresting. For a long wormhole, it looked like traveling through a long tunnel with walls whizzing past, too much like things we’ve seen in movies before. Chris showed me many variants with many bells and whistles, and I had to agree that none had the compelling freshness that he wanted. After sleeping on it, I still had no magic-bullet solution.
The next day Chris flew to London and closeted himself with Paul’s Double Negative team, searching for a solution. In the end, they were forced to abandon my wormhole equations and, in Paul’s words, “go for a much more abstract interpretation of the wormhole’s interior,” an interpretation informed by simulations with my equations, but altered significantly to add artistic freshness.
When I experienced the wormhole trip in an early screening of Interstellar , I was pleased. Though not fully accurate, it captures the spirit and much of the feel of a real wormhole trip, and it’s fresh and compelling.
What did you think?
16
Discovering the Wormhole: Gravitational Waves

How might humans have discovered Interstellar ’s wormhole? As a physicist, I have a favorite way. I describe it here in an extrapolation of Interstellar ’s story—an extrapolation that, of course, is my own and not Christopher Nolan’s.
LIGO Detects a Burst of Gravitational Waves
I imagine that decades before the movie begins, when Professor Brand was in his twenties, he was deputy director of a project called LIGO: The Laser Interferometer Gravitational Wave Observatory (Figure 16.1). LIGO was searching for ripples in the shape of space arriving at Earth from the distant universe. These ripples, called gravitational waves, are produced when black holes collide with each other, when a black hole tears a neutron star apart, when the universe was born, and in many other ways.
Читать дальше
















