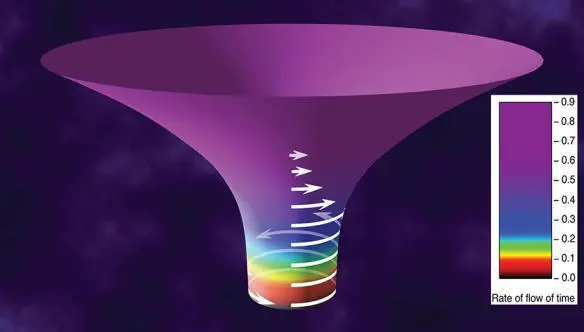
Fig. 5.5. Precise depiction of the warped space and time around a rapidly spinning black hole: one that spins at 99.8 percent of the maximum possible rate. [Drawing by Don Davis based on a sketch by me.]
In the fully accurate Figure 5.5, I don’t depict the hole’s interior. We’ll get to that later, in Chapters 26 and 28.
The warping in Figure 5.5 is the essence of a black hole. From its details, expressed mathematically, physicists can deduce everything about the black hole, except the nature of the singularity at its center. For the singularity, they need the ill-understood laws of quantum gravity (Chapters 26).
A Black Hole’s Appearance from Inside Our Universe
We humans are confined to our brane. We can’t escape from it, into the bulk (unless an ultra-advanced civilization gives us a ride in a tesseract or some such vehicle, as they do for Cooper in Interstellar ; see Chapter 29). Therefore, we can’t see a black hole’s warped space, as depicted in Figure 5.5. The black-hole funnels and whirlpools so often shown in movies, for example, Disney Studios’ 1979 movie The Black Hole , would never be seen by any creature that lives in our universe.

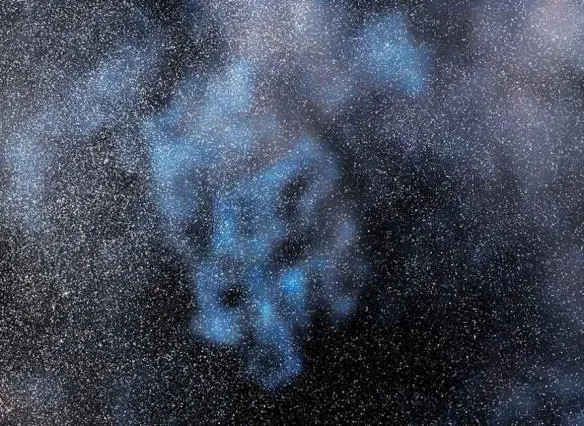
Fig. 5.6. A fast-spinning black hole ( left ) moving in front of the star field shown on the right. [From a simulation for this book by the Double Negative visual-effects team.]
Interstellar is the first Hollywood movie to depict a black hole correctly, in the manner that humans would actually see and experience it. Figure 5.6 is a example, not taken from the movie. The black hole casts a black shadow on the field of stars behind it. Light rays from the stars are bent by the hole’s warped space; they are gravitationally lensed , producing a concentric pattern of distortion. Light rays coming to us from the shadow’s left edge move in the same direction as the hole’s whirling space. The space whirl gives them a boost, letting them escape from closer to the horizon than light rays on the shadow’s right edge, which struggle against the whirl of space. That’s why the shadow is flattened on the left and bulges out on the right. In Chapter 8 I talk more about this and other aspects of what a black hole really looks like, as seen up close in our universe, in our brane .
How Do We Know This Is True ?
Einstein’s relativistic laws have been tested to high precision. I’m convinced they are right, except when they confront quantum physics. For a big black hole like Interstellar ’s Gargantua, quantum physics is relevant only near its center, in its singularity. So if black holes exist at all in our universe, they must have the properties that Einstein’s relativistic laws dictate, the properties I described above.
These properties and others have been deduced from Einstein’s equations by a large number of physicists standing intellectually on each others’ shoulders (Figure 5.7); most importantly, Karl Schwarzschild, Roy Kerr, and Stephen Hawking. In 1915, shortly before his tragic death on World War I’s German/Russian front, Schwarzschild deduced the details of the warped spacetime around a nonspinning black hole. In physicists’ jargon, those details are called the “Schwarzschild metric.” In 1963, Kerr (a New Zealand mathematician) did the same for a spinning black hole: he deduced the spinning hole’s “Kerr metric.” And in the early 1970s Stephen Hawking and others deduced a set of laws that black holes must obey when they swallow stars, collide and merge, and feel the tidal forces of other objects.
Black holes surely do exist. Einstein’s relativistic laws insist that, when a massive star exhausts the nuclear fuel that keeps it hot, then the star must implode. In 1939, J. Robert Oppenheimer and his student Hartland Snyder used Einstein’s laws to discover that, if the implosion is precisely spherical, the imploding star must create a black hole around itself, and then create a singularity at the hole’s center, and then get swallowed into the singularity. No matter is left behind. None whatsoever. The resulting black hole is made entirely from warped space and time. Over the decades since 1939, physicists using Einstein’s laws have shown that if the imploding star is deformed and spinning, it will also produce a black hole. Computer simulations reveal the full details.
Astronomers have seen compelling evidence for many black holes in our universe. The most beautiful example is a massive black hole at the center of our Milky Way galaxy. Andrea Ghez of UCLA, with a small group of astronomers that she leads, has monitored the motions of stars around that black hole (Figure 5.8). Along each orbit, the dots are the star’s position at times separated by one year. I marked the black hole’s location by a white, five-pointed symbol. From the stars’ observed motions, Ghez has deduced the strength of the hole’s gravity. Its gravitational pull, at a fixed distance, is 4.1 million times greater than the Sun’s pull at that distance. This means the black hole’s mass is 4.1 million times greater than the Sun’s!

Fig 5.7. Black-hole scientists. Left to right : Karl Schwarzschild (1873–1916), Roy Kerr (1934– ), Stephen W. Hawking (1942– ), J. Robert Oppenheimer (1904–1967), and Andrea Ghez (1965– ).
Figure 5.9 shows where this black hole is on the night sky in summer. It is to the lower right of the constellation Sagittarius, the teapot, at the × labeled “Galactic Center.”
A massive black hole inhabits the core of nearly every big galaxy in our universe. Many of these are as heavy as Gargantua (100 million Suns), or even heavier. The heaviest yet measured is 17 billion times more massive than the Sun; it resides at the center of a galaxy whose name is NGC1277, 250 million light-years from Earth—roughly a tenth of the way to the edge of the visible universe.
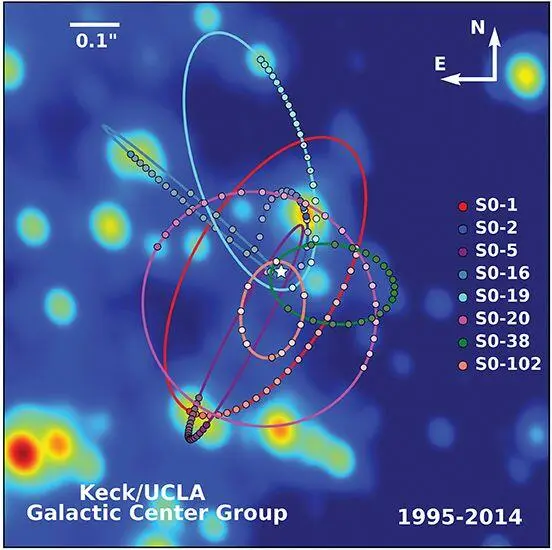
Fig. 5.8. Observed orbits of stars around the massive black hole at the center of our Milky Way galaxy, as measured by Andrea Ghez and colleagues.

Fig. 5.9. The location of our galaxy’s center on the sky. A giant black hole resides there.
Inside our own galaxy, there are roughly 100 million smaller black holes: holes that typically are between about three and thirty times as heavy as the Sun. We know this not because we’ve seen evidence for all these, but because astronomers have made a census of heavy stars that will become black holes when they exhaust their nuclear fuel. From that census, astronomers have inferred how many such stars have already exhausted their fuel and become black holes.
So black holes are ubiquitous in our universe. Fortunately, there are none in our solar system. If there were, the hole’s gravity would wreak havoc with the Earth’s orbit. The Earth would be thrown close to the Sun where it boils, or far from the Sun where it freezes, or even out of the solar system or into the black hole. We humans would survive for no more than a year or so!
Читать дальше


















