Так как определенность предмета и отношений есть положенная определенность, то дальнейшие операции с ними тоже совершенно аналитичны, и в аналитической науке имеются поэтому не столько теоремы , сколько задачи . Аналитическая теорема содержит в себе задачу уже как решенную самоё по себе, и совершенно внешнее различие, присущее тем двум сторонам теоремы, которые в ней приравниваются друг к другу, столь несущественно, что такая теорема должна была бы показаться тривиальным тождеством. Кант, правда, объявил предложение «5 + 7 = 12» синтетическим предложением на том основании, что одно и то же содержание на одной стороне представлено в форме нескольких чисел, в форме 5 и 7, а на другой стороне в форме одного числа, в форме 12 (258). Однако, если аналитическое предложение не должно означать совершенно абстрактно тождественное и тавтологическое «12 = 12» и в нем вообще должно быть некоторое движение вперед, то должно быть налицо какое–нибудь различие, но такое различие, которое не основывается ни на каком качестве, ни на какой определенности рефлексии и тем паче ни на какой определенности понятия. «5 + 7» и «12» суть совершенно то же самое содержание; в первой стороне равенства выражено также и требование , чтобы 5 и 7 были сочетаны в одном выражении; а это означает, что, подобно тому как 5 есть нечто сосчитанное, причем прекращение счета на этом числе было совершенно произвольным и счет мог бы с таким же успехом быть продолжен и дальше, так теперь следует считать дальше с условием, чтобы число долженствующих быть прибавленными единиц равнялось 7. «12» есть, следовательно, результат 5 и 7 и такого действия, которое здесь уже положено и по своей природе тоже есть некоторое совершенно внешнее, чуждое мысли дело, так что этот результат может поэтому быть осуществлен также и машиной. Здесь нет ни малейшего перехода к некоторому другому ; это просто процесс продолжения, т. е. повторения того же самого действия, через которое произошли 5 и 7.
Доказательство такой теоремы — она требовала бы доказательства, если бы она была синтетическим предложением, — состояло бы лишь в операции определенного 7-ью дальнейшего сосчитывают начиная с 5-ти и в познании совпадения результата этого дальнейшего счета с тем, что и в других случаях называется 12-ью и что в свою очередь есть не что иное, как именно само это определенное дальнейшее сосчитывание. Поэтому вместо формы теоремы сразу же берут форму задачи , требования действия, а именно, высказывается лишь одна сторона того уравнения, которое составило бы теорему, другая же сторона этого уравнения должна быть найдена путем решения этой задачи. Задача заключает в себе содержание и указывает то определенное действие, которое должно быть произведено над ним. Действие не ограничено каким–либо неподатливым, наделенным специфическими отношениями материалом, а представляет собой внешнюю субъективную операцию, и материал безразлично принимает те определения, которые в нем полагаются этим действием. Вся разница между поставленными в задаче условиями и полученным в решении результатом состоит лишь в том, что в последнем действительно произведено соединение или разъединение тем определенным образом, как было указано в задаче.
Применение здесь формы геометрического метода, относящегося к синтетическим предложениям, и присоединение вслед за решением задачи также и доказательства представляют собой поэтому совершенно излишнее сооружение. Это доказательство не может выразить ничего другого, кроме той тавтологии, что решение правильно, потому что действие произведено так, как было задано. Если задача требует сложить несколько чисел, то решение состоит в том, что их действительно складывают; доказательство же показывает, что решение правильно, потому что было задано сложить и было произведено сложение. Если задача заключает в себе более сложные определения и действия, скажем, например, перемножить десятичные числа (258), а решение не указывает ничего, кроме механического приема, то в этом случае, действительно, требуется доказательство; но это доказательство не может состоять ни в чем другом, как только в анализе тех определений и действий, из которых решение получается само собой. В силу этого отделения решения , как некоторого механического приема, от доказательства , как припоминания природы подлежащего действию предмета и самого действия, как раз утрачивается преимущество аналитической задачи, заключающееся в том, что построение непосредственно выводится из задачи и потому само по себе может быть изложено как понятное для рассудка , между тем как, действуя иначе, мы ясно выраженным образом сообщаем построению недостаток, свойственный синтетическому методу. — В высшем анализе, где, главным образом в связи со степенным отношением, появляются качественные и зависящие от понятийных определенностей отношения дискретных величин, задачи и теоремы, действительно, содержат в себе синтетические определения; там приходится брать в качестве средних членов другие определения и отношения, чем те, которые непосредственно указаны задачей или теоремой. Однако и эти вспомогательные определения непременно должны быть такого рода, чтобы они имели свое основание в том, что здесь принимается в соображение и развивается одна из сторон задачи или теоремы; то обстоятельство, что они выглядят синтетическими, происходит исключительно оттого, что задача или теорема сама не называет наперед этой стороны. — Задача, например, найти сумму степеней корней уравнения решается посредством рассмотрения и затем соединения функций, представляющих собой коэфициенты уравнения корней. Взятое здесь в помощь определение функций коэфициентов и соединения этих функций не выражено наперед в задаче, но во всем прочем само развертывание совершенно аналитично. Подобным же образом решение уравнения 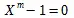 с помощью синусов, а также имманентное, как известно, найденное Гауссом (258) алгебраическое решение при помощи рассмотрения остатка от делениях
с помощью синусов, а также имманентное, как известно, найденное Гауссом (258) алгебраическое решение при помощи рассмотрения остатка от делениях 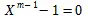 на m и так называемых первообразных корней — одно из важнейших расширений анализа новейшего времени — есть синтетическое решение, так как использованные тут вспомогательные определения (синусы или рассмотрение остатков) не являются определениями самой задачи.
на m и так называемых первообразных корней — одно из важнейших расширений анализа новейшего времени — есть синтетическое решение, так как использованные тут вспомогательные определения (синусы или рассмотрение остатков) не являются определениями самой задачи.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

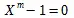 с помощью синусов, а также имманентное, как известно, найденное Гауссом (258) алгебраическое решение при помощи рассмотрения остатка от делениях
с помощью синусов, а также имманентное, как известно, найденное Гауссом (258) алгебраическое решение при помощи рассмотрения остатка от делениях 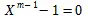 на m и так называемых первообразных корней — одно из важнейших расширений анализа новейшего времени — есть синтетическое решение, так как использованные тут вспомогательные определения (синусы или рассмотрение остатков) не являются определениями самой задачи.
на m и так называемых первообразных корней — одно из важнейших расширений анализа новейшего времени — есть синтетическое решение, так как использованные тут вспомогательные определения (синусы или рассмотрение остатков) не являются определениями самой задачи.






