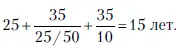Галина Маховикова - Экономическая теория. Завтра экзамен

Задача 2. При использовании первой конструкции разница составит 720 тыс. руб. (150 x12 x 25 x 20) – (300 – 120), а при использовании второй – 520 тыс. руб. (150 x 12 x 20 x 20) – (220 – 120). Первая конструкция выгоднее, несмотря на то что она дороже.

Задача 3. Величина оборотного капитала: 30 + 10 + (2 x 6) = $52. Оборот оборотного капитала за год: 52 x 2 = 104. Число оборотов в течение года: п = 104 / 52 = 2 оборота.

Задача 4. Время оборота основного капитала:

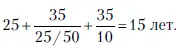
Задача 5. Годовая величина амортизационных отчислений зданий: 200/20 = $10, машин и оборудования: 100 / 10 = $10, общая годовая амортизация: 10 + 10 = $20. Авансированный основной капитал: 200 + + 100 = $300. Время оборота: 300 / 20 = 15 лет.

Задача 6. Материальный износ за 3 года = (200 / 10) х 3 = $60. Моральный износ = (200 – 180) / 10 х (10 – 2) = $16.

Задача 7. а) Амортизационные отчисления за 4 года: А = (2000 / 10) х х 4 = 800 руб. Норма амортизации – 10 %; б) применяется двойная норма – 20 % к остаточной стоимости станка. Амортизационные отчисления за год: А = 20 % от 2000 руб. = 400 руб.

Задача 8. Величина оборотного капитала: 460 – 70 – 50 – 100 = $240, в том числе стоимость машин – $180, зданий – $60. Величина амортизации через 7 лет: А = (180 / 18) х 7 + (60 / 30) х 7 = $84.

Задача 1. Бухгалтерская прибыль = 900 – х, где х – явные издержки: х = 900 – 400 = 500 тыс. ден. ед. Чистая экономическая прибыль = = 900 – (500 + у), где у – неявные издержки 150 = 900 – (500 + у) 900 – 500 – 150 = 250.

Задача 2. Бухгалтерские издержки = 20 + 8 = 28 тыс. ден. ед. Экономические издержки = 28 + 5 + 12 + 30 = 75 тыс. ден. ед.

Задача 3. При Q = 0, FC = TC = 60, VC = TC – FC = 0; при Q = 1 VC = = 140 – 60 = 80, MC = VC 1+1– VC. Отсюда МС при увеличении выпуска от 0 до 1 равны 80 – 0 = 80 и т. д. При Q = 2, VC = 120, MC = 40. При Q = 3, VC = 180, MC = 60. При Q = 4, VC = 360, MC = 180.

Задача 1. Используем формулу бюджетного ограничения: 1 = P xx + P yy. Если весь доход потребитель расходует на приобретение товара «у», то его доход: 1 = Р кО + 500 – 20 = 10 000 руб. При расходовании всей суммы дохода на приобретение товара «х» Р х= 1/X max= 10 000: 25 = = 400 руб. Уравнение бюджетной линии: у = 10 000: 500 – (400: 500) х у = = 20 – 0,8х. Наклон бюджетной линии равен отношению цен товаров, взятому со знаком минус, т. е. -0,8.

Задача 2. Для определения координат линии спроса надо знать две величины: цену и соответствующий ей объем спроса. На основе формулы бюджетного ограничения рассчитываются цены товара «х»: Р х1=1/Х max1= 10 000 / 20 = 500 руб. P x2= 1: X max2= 10 000 / 40 = 250 руб.

Координаты двух точек линии спроса на товар Х: (500: 10) и (250: 15).

Задача 1. Надо сопоставить ожидаемую норму прибыли с разными уровнями процентной ставки. Если эта ставка меньше 12 %, имеет смысл осуществить проект. При 13 % – лучше поместить деньги в банк.

Задача 2. Реальная ставка процента: 12 % – 7 % = 5 %. Если сравнить ожидаемую норму прибыли, т. е. 7 %, с реальной ставкой – 5 %, то проект капиталовложения окажется возможным.

Задача 3. Бухгалтерская прибыль = 500 – (250 + 70) = 180 тыс. ден. ед.

Задача 4. Банковская прибыль = (2000 х 4) / 100 (1700 х 2) / 100 – 5 = = 80 – 30 – 5 = 45 тыс. ден. ед. (45 х 100) / 300 + 15 %.

Задача 5. 5 % – 3 % – 10 % = -8%. Реальная зарплата понизилась на

8%.

Задача 6. Цена земельного участка: 60 тыс. х 100 % / 10 = 600 тыс. ден. ед.

Задача 7. Земельная рента = 8000 – (50 000 / 10) – (5 х 50 000 / 100) = = 500 ден. ед.

Задача 8. Годовые затраты фирмы 500 + 200 = 700 тыс. руб. Годовая выручка 225 х 12 мес. = 2700 тыс. руб. Производство прибыльно.

Задача 1. Дефлятор ВНП = (100 000 х 100) + (75 000 х 150) + (50 000 х х 75) / (100 000 х 60) + (75 000 х 90) + (50 000 х 80) = 1,49.

Задача 2. Дефлятор ВНП = номинальный ВНП / реальный ВНП х

х 100 %. Лекция 14

Задача 1. Мультипликатор = К = 1 / 1 – 5/7 = 3,5. Общий прирост национального дохода = 1000 х 3,5 = 3500 единиц.

Задача 2. Сбережения = 40 + 20 + 30 + 70 – 10 – 20 – 30 = 100.

Задача 3. Вопрос подразумевает рассуждения. Важна аргументация.

Задача 4. 490 – 466 / х = 24/х = 4, х = 6.

Задача 5. МРС = 1 – 0,25 = 0,75; 1680 = 100 + 0,75 ВЕП + х + 200 + 70; х = 50.

Задача 1. а) Определим вначале равновесный объем продаж и равновесную цену без учета налога. Ответ: равновесная цена – 5 руб., равновесный объем – 4 млн шт. Поскольку потоварный налог уплачивает продавец, то цена для него составит р -= р +– 1,5, где р +– цена, которую платит покупатель. Подставим теперь данное равенство в функцию предложения и определим равновесный объем продаж (Q E) и цены для покупателя (р +) и продавца (р -). Ответ: р += 6 руб., р - = 4,5 руб., Q E= 3 млн шт.

б) Если налог задан в процентах от цены, то: р -= р +– 0,25р+. Ответ:

р += 6 руб., р -= 4,5 руб., Q E= 3 млн шт.