Вячеслав Кириллов - Логика - учебник для юридических вузов

1-я и 4-я строки таблицы показывают, что Аи Водновременно принимают одинаковые значения — Ии Л; зачеркнутые 2-я и 3-я строки показывают, что эквивалентные суждения одновременно не могут принимать различные значения.

Отношение эквивалентности позволяет выражать одни сложные суждения через другие — конъюнкцию через дизъюнкцию или импликацию и наоборот. Приведем четыре известные эквивалентности, которые являются законами логики.

1) Выражение конъюнкции через дизъюнкцию:

˥(A ∧ B) ≡ ˥A ∨ ˥B

2) Выражение дизъюнкции через конъюнкцию:

˥(A ∨ B) ≡ ˥A ∧ ˥B

Эти две эквивалентности называются законами де Моргана.

3) Выражение импликации через конъюнкцию:

˥(A → B) ≡ (A ∧ ˥B)

4) Выражение импликации через дизъюнкцию:

A → B ≡ ˥A ∨ B

2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

Отношение частичной совместимости для сложных суждений показано в таблице 9, где Аи В— схемы сложных суждений; ∨— знак частичной совместимости. 1-я строка таблицы говорит об одновременной истинности Аи В; 2-я и 3-я — несовпадение значений; 4-я строка зачеркнута, поскольку исключается одновременная ложность Аи В.

3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным.

В таблице 10 показано отношение подчинения между сложными суждениями: Аи В— схемы суждений; → — знак подчинения. 1-я строка показывает, что в случае истинности Аистинным является и В. В 3-й и 4-й строках Аявляется ложным, а Впринимает произвольные значения. 2-я строка в таблице зачеркнута, поскольку отношение подчинения исключает ложность подчиненного Впри истинности подчиняющего А.

Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующею все виды рассуждений.

Несовместимыми являются суждения, которые одновременно не могут быть истинными. Это противоположность и противоречие.

1. Противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.

В таблице 11 показано отношение противоположности между суждениями: Аи В— схемы суждений; ∧ — знак логической противоположности. 1-я строка таблицы зачеркнута. Это означает, что оба суждения одновременно не могут быть истинными; 2-я и 3-я строки показывают, что суждения могут принимать исключающие значения; 4-я строка — оба суждения могут быть ложными. Это значит, что при ложности одного из противоположных суждений нельзя установить значения другого: оно может быть как истинным, так и ложным.

2. Противоречие — отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое ложно, а при ложности первого второе истинно.

Противоречащие отношения между сложными суждениями показаны в таблице 12; Аи В— схемы сложных суждений, ∨ — знак отношения противоречия.

Таблица 11

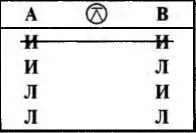
Таблица 12

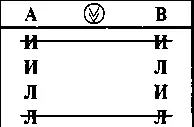
Вычеркнутые 1-я и 4-я строки показывают, что Аи Вмогут принимать лишь альтернативные значения.

Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию. Так, например, для рпротиворечащим будет ˥р; для конъюнкции р ∧ qпротиворечием будет ее отрицание — ˥(р ∧ q)и т. п.

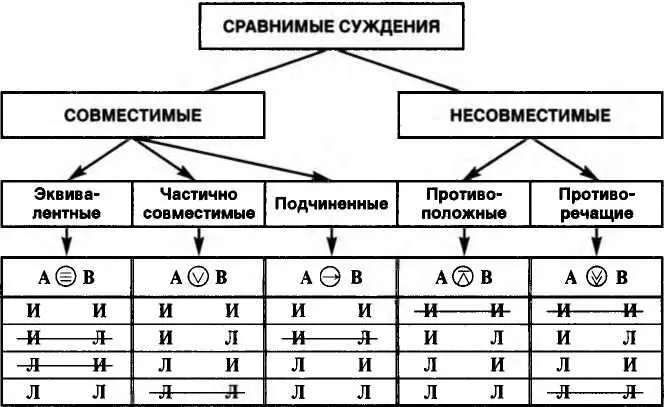
Обобщенная таблица логических отношений между сложными суждениями (таблица 13).

Таблица 13

Отчетливое представление об отношениях, в которых могут находиться суждения, позволяет логически грамотно анализировать высказывания участников дискуссий. Бывают ситуации, когда логический анализ показывает совместимость различных по структуре суждений. Нередко это случается с частными суждениями. Пропонент утверждает, что «Некоторые S есть Р»; оппонент настаивает, что «Некоторые S не есть Р». На поверку же выходит, что эти суждения не исключают друг друга, а являются частично совместимыми и оба могут оказаться истинными.