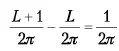 – для Земли,
– для Земли,
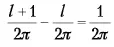 – для апельсина.
– для апельсина.
Этот поразительный результат является следствием постоянства отношения длины окружности к ее радиусу.
151. Может показаться, что последний кусок материи будет отрезан по истечении 8 дней, ведь 16: 2 = 8. На самом же деле последний кусок отрезается по истечении семи дней. Ко второму дню кусок материи станет равным 14 метрам. К седьмому дню от него останется 4 метра, следовательно последний раз 2 метра будет отрезано как раз на седьмой день. На восьмой же день от куска материи останется всего 2 метра.
152.
153. Сначала может показаться, что колесо может вращаться как по часовой стрелке, так и против нее, ведь текущая вода реки с одинаковой силой давит на все его лопасти. Однако нижние слои воды, испытывая на себе давление верхних, движутся с меньшей скоростью, а выше лежащие слои воды перемещаются быстрее. Следовательно, они оказывают большее давление на лопасти колеса, которое, таким образом, будет вращаться по часовой стрелке.
154. На первый взгляд кажется, что Иванов должен получить 3 рубля, а Сидоров – 5 рублей. Однако 8 рублей было уплачено не за 8 поленьев (по 1 рублю за полено), а только за третью часть от 8 поленьев, так как трое соседей пользовались огнем в одинаковой мере. Следовательно, 8 поленьев были оценены в 8 x 3 = 24 рубля, и одно полено стоит 3 рубля. Стало быть, Иванов за свои 3 полена должен получить 9 рублей, но он сам воспользовался плитой на 8 рублей, значит, ему причитается всего 9–8 = 1 рубль; а Сидоров за свои 5 поленьев должен получить 15 рублей, на при вычитании из них 8 рублей за использование общей плиты, ему остается 7 рублей. Итак, из уплаченных Петровым 8 рублей Иванов должен взять себе 1 рубль, а Сидоров – 7 рублей.
155. Может показаться, что круги на воде от камня, брошенного в быструю реку, будут вытягиваться в направлении течения и иметь форму эллипсов. В действительности это не так. На поверхности реки волны будут иметь круговую форму, как и на неподвижной водной поверхности. Когда вода течет, то перемещается каждаяее точка, и происходит то, что в геометрии называется «параллельным переносом»: любая фигура перемещается на новое место, но сама нисколько не меняется (круги остаются кругами).
156. Кажется, что такого числа, кроме нуля, не существует. На самом же деле оно есть. Это произведение всех чисел. Вопрос задачи сформулирован так, что побуждает нас искать какое-то конкретное, определенное и конечное число. Но в данном вопросе нет никакого подвоха. Когда мы пытаемся найти определенное число, то сами ставим себя в некие рамки, ограничивая или суживая диапазон своего поиска, ведь числом является любая величина, в том числе и неопределенная, и бесконечно большая. Произведение всех чисел – это тоже число, только бесконечно большое. Такое число, разумеется, делится на все числа (т. е. на все свои множители) без остатка.
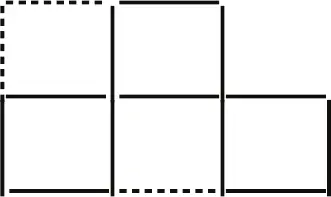
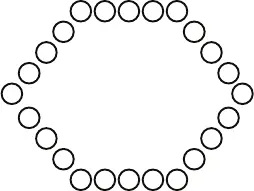
157. На первый взгляд такое расположение людей невозможно, ведь 24: 6 = 4, т. е. в каждом ряду может быть по 4, а не по 5 человек. Однако в условии задачи ничего не сказано о расположении искомых рядов, следовательно, оно может быть произвольным. Людей можно расположить так:
158. Если внимательно прочитать условие задачи, то можно заметить, что отец в будущем никогда не будет в шесть раз старше сына, потому что такое соотношение их возрастов могло быть только в прошлом. Однако задачу вполне можно решить, не замечая этой особенности, с помощью простого уравнения. Примем искомый срок за x. Тогда спустя этот срок отцу будет 32 + x лет, а сыну 5 + x лет. Так как отец в это время должен быть в шесть раз старше сына (по условию), то можно составить уравнение:
32 + x = 6 (7 + x)
преобразуем:
32 + x = 42 + 6x
32 – 42 = 6x – x
– 10 = 5x
x = – 10 : 5
x = – 2
Результат решения уравнения на первый взгляд получается довольно странным: отец будет старше сына в шесть раз через «минус два года». На самом же деле ничего странного нет: через «минус два года» означает не что иное, как «два года назад». И действительно, два года назад отцу было 30 лет, а сыну 5 лет, и первый был в шесть раз старше второго. Как то ни удивительно, но уравнение оказалось «внимательнее» нас, «заметив» то, чего не заметили мы.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

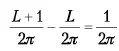 – для Земли,
– для Земли,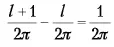 – для апельсина.
– для апельсина.












