Дмитрий Гусев - Логика. Учебное пособие

Для того, чтобы предотвратить возможные негативные последствия употребления неопределенных понятий, в их содержание вводятся дополнительные признаки, благодаря чему оно (содержание) становится ясным, а объем понятия – резким. Например, желая преодолеть неопределенность понятия молодая семья , можно ввести в его содержание признак – «супругам не более 30 лет». Так же неопределенное понятие опытный специалист возможно превратить в определенное, добавляя к его содержанию признак – «стаж работы в данной области не менее 10 лет». Однако, в этом случае дополнительный признак выбирается произвольно: почему бы не считать молодой ту семью, в которой супругам не более 25 лет или же не более 35 лет, точно так же возможно утверждать, что опытный специалист – это тот, кто проработал в данной области не менее 5 лет или же не менее 15 лет, или даже – 20 лет. Таким образом, проясняющий признак для содержания неопределенного понятия всегда относителен, т. к. зависит от договоренности между людьми в каждой конкретной ситуации, в силу чего превратить неопределенное понятие в определенное, по крупному счету, невозможно: неопределенное понятие, в конечном итоге, остается неопределенным.

Между понятиями, а вернее между их объемами, существуют определенные отношения, знание которых является в логике одним из наиболее важных (можно сказать, что виды отношений между понятиями в логике – это примерно то же самое, что в математике таблица умножения). Обычно понятия делят на сравнимые( например, Москва и столица России, писатель и россиянин, город и населенный пункт, лев и тигр, горячая вода и холодная вода, высокий человек и невысокий человек ) и несравнимые(например, пингвин и кирпич, треугольник и президент, учебное заведение и небесное тело, спортсмен и город, книга и небоскреб, растение и государство ).

Сравнимые понятия бывают совместимымии несовместимыми. Совместимыминазываются понятия, объемы которых имеют общие элементы, каким-либо образом соприкасаются. Например, понятия спортсмен и американец совместимые, т. к. их объемы имеют общие элементы, или объекты: есть такие спортсмены, которые являются американцами и, наоборот, есть такие американцы, которые являются спортсменами. Несовместимыминазываются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Например, понятия треугольник и квадрат являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом и наоборот.

Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения.

Понятия находятся в отношении равнозначностив том случае, если их объемы полностью совпадают. Например, равнозначными будут поняти я квадрат и равносторонний прямоугольник , т. к. любой квадрат – это равносторонний прямоугольник, а любой равносторонний прямоугольник – это квадрат. В логике принято изображать отношения между понятиями с помощью круговых схем Эйлера (известный математик XVIII века): одно понятие, а вернее его объем, изображается одним кругом, а второе, т. е. его объем – другим. Взаимное расположение этих кругов на схеме (они могут полностью совпадать или пересекаться, или не соприкасаться, или один круг располагается внутри другого) и показывает то или иное отношение между понятиями. Так отношение равнозначности между понятиями квадрат и равносторонний прямоугольник изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают:

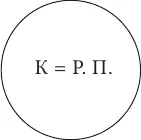
Понятия находятся в отношении пересечениятогда, когда их объемы совпадают только частично. Например, пересекающимися будут понятия школьник и спортсмен : есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий):

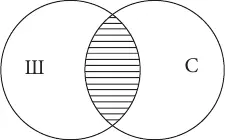
Понятия находятся в отношении подчиненияв том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия карась и рыба , т. к. все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим – родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого: