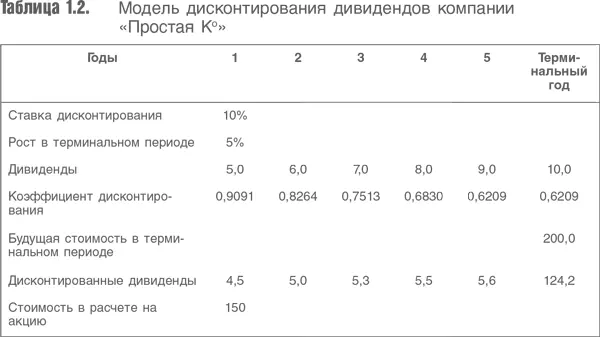
1 ...6 7 8 10 11 12 ...161 PV = FV / (1+k) n,
где PV – приведенная стоимость, FV – будущая стоимость, k – ставка дисконтирования, n – количество лет.
Заметьте, что конечная стоимость дисконтируется на пять, а не на шесть лет, хотя она основана на величине дивиденда года 6. Это объясняется тем, что в модели Гордона в качестве первого члена используется величина, которая ожидается спустя год. Таким образом, денежный поток, который начинается на году 6, учитывается как величина, относящаяся к году 5, затем мы должны привести ее к текущей стоимости путем дисконтирования на пять лет.
К сожалению, в подавляющем большинстве моделей оценки, применяемых в банках, инвестиционных и производственных компаниях, этим и ограничиваются. Конечно, эти модели корректируются, поскольку компании могут финансироваться путем заимствований или увеличения акционерного капитала (к этому вопросу мы еще вернемся), включать в свою отчетность нематериальные активы, запасы и другие элементы (часто неудачно – этот вопрос мы рассмотрим позже). Но в принципе, большинство работают именно так, и в этой простоте кроется опасность.
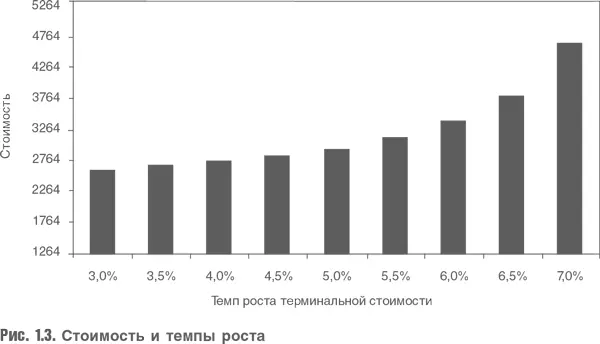
Вернемся к компании «Постоянный рост К°» и изменим темп роста, учитываемый при расчете терминальной стоимости (рис. 1.3).
Минимальное изменение темпа роста резко меняет оценку стоимости, часть стоимости в размере 1264 составит сумма дивидендов за 25 лет прогнозного периода, поэтому столбцы отражают изменение стоимости за счет темпов роста в постпрогнозном периоде. Но разве это возможно? Чтобы ответить на этот вопрос, рассмотрим компоненты модели Гордона: дивиденды, темп роста и ставка дисконтирования. На самом деле мы меняем темп роста, оставляя другие компоненты неизменными. Насколько это оправданно? Может ли темп роста компании изменяться, но при этом компания распределяет один и тот же объем дивидендов? Конечно, нет. Если мы хотим расти быстрее, то должны реинвестировать большую часть прибыли в расширение бизнеса. Другая крайность: выплатить всю прибыль в виде дивидендов, при этом темп роста будет нулевым. В нашем первом расчете мы предполагали, что варианты выглядят примерно так, как на рис. 1.4. В наших вычислениях мы предполагали, что темп роста компании изменяется, а объем реинвестированной прибыли остается неизменным, что выглядит довольно странно.
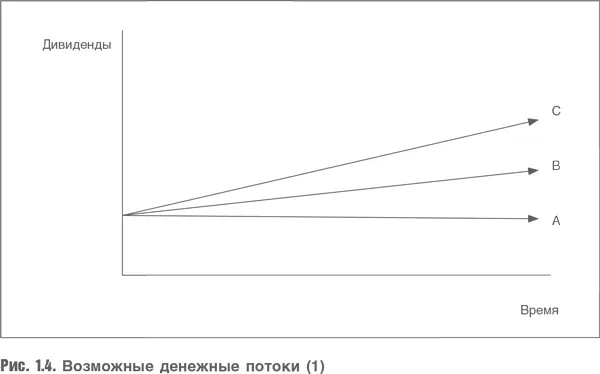
Но реальность такова: если компания хочет расти быстрее, она должна реинвестировать бóльшую часть своей прибыли. И если она выплачивает бόльшую часть прибыли в виде дивидендов, то это неизбежно приведет к более низким темпам роста. Поэтому реальная картина выглядит так, как показано на рис. 1.5.
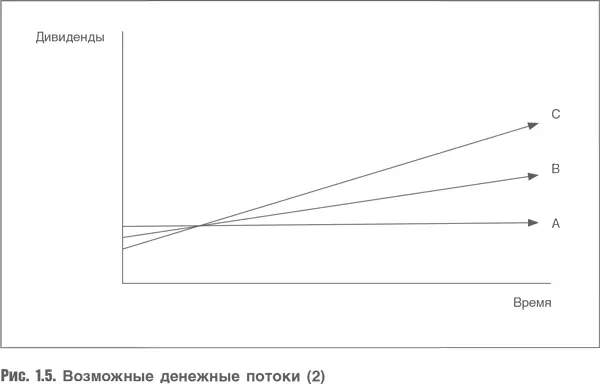
Возникает выбор. Либо распределяем бóльшую долю прибыли в виде дивидендов, но при этом темп роста будет более низким, либо получаем меньше от компании сегодня с целью больше реинвестировать, при этом ожидая более высоких темпов роста доходов в будущем. От чего зависит выбор? От доходности, которую мы получим на дополнительный инвестированный капитал. Данную взаимосвязь выражает формула (доказательство см. в Приложении):
g = b × R,
где g – темп роста, b – доля реинвестируемой прибыли, R – доходность вновь привлекаемого акционерного капитала.
Заметьте, что доходность вновь привлекаемого акционерного капитала не обязательно должна совпадать с доходностью существующего акционерного капитала. Предположим, мы имеем бизнес, дающий фантастические доходы – например, идеально расположенные фешенебельные магазины. Может случиться так, что они будут продолжать приносить высокие доходы без увеличения инвестиций. Но если мы решаем инвестировать часть прибыли в новые объекты (возможно, менее привлекательные), то доходность вновь привлекаемого акционерного капитала будет ниже, чем доходность старого. Это доходность дополнительного капитала, который генерирует дополнительную прибыль.
Обычно мы размышляем об этом, подходя к вопросу с другой стороны. Вместо того чтобы устанавливать долю нераспределенной прибыли, иногда разумнее устанавливать темп роста и доходность, а по ним определять долю нераспределенной прибыли. Тогда:
Читать дальше
Конец ознакомительного отрывка
Купить книгу
















