Юрген Аппело - Agile-менеджмент. Лидерство и управление командами

2. Клетка остается живой при условии, что живы две или три ее соседки, что можно интерпретировать как наличие достаточных ресурсов для продолжения ее существования.

3. Клетка умирает или остается мертвой во всех остальных случаях, что соответствует перенаселенности (слишком много соседей) или нехватке ресурсов (слишком мало соседей).

Правила непрерывно применяются ко всем клеткам одновременно. В результате возникает последовательность поколений системы, а пассивному игроку остается только потрясенно наблюдать за возникновением замысловатых конфигураций. Мне нравится эта игра, поскольку только в ней мне все время удается выигрывать.

Конвей протестировал множество различных наборов правил. При определенных правилах поле всегда целиком покрывается живыми клетками. При других наступает коллапс, и все клетки, существовавшие в первоначальной конфигурации, вымирают. В конечном итоге Конвей остановил свой выбор на наборе правил, который приводит к возникновению устойчивых конфигураций (в варианте, показанном на рис. 8.1, это происходит всего через три этапа).

Такая устойчивая конфигурация (иногда она возникает после сотен или даже тысяч поколений) может состоять из набора неподвижных объектов («натюрморт»), бесконечно повторяющихся циклов изменений («осцилляторы») или «планеров» (группы объектов, перемещающиеся по решетке).

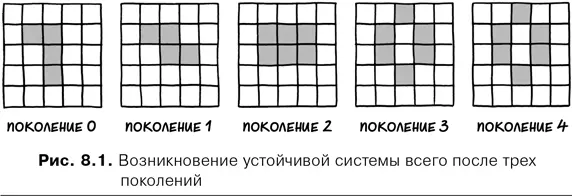
«Жизнь» – это пример клеточных автоматов, то есть математических систем, в которых клетки подвергаются воздействию других клеток в соответствии с заранее установленными правилами. Она представляет особый интерес, поскольку является прекрасной демонстрацией того, как система, в которой действует простой набор правил, может тем не менее проявлять чрезвычайно сложное поведение.

Игра также показывает, что независимо от исходной конфигурации систему в конечном итоге всегда можно стабилизировать. Есть лишь одна тонкость, которую необходимо учитывать: чтобы стабилизировать систему, правила должны быть подобраны определенным образом. Значит ли это, что для возникновения устойчивых систем нужен дизайнер? И значит ли это, что для более тонкой настройки правил нужны менеджеры? Звучит убедительно (с точки зрения менеджеров).

Наблюдение, что правила должны подбираться определенным образом, чтобы система стабилизировалась, оставаясь при этом живой, очень важно. Измените правила, и вы получите другую систему с другим поведением. «Жизнь» – лишь один из миллиардов клеточных автоматов, многие из которых «мертвы», скучны или ведут себя хаотически.

В одной из своих работ, оказавшей значительное влияние на других исследователей, Стивен Вольфрам, основатель первого научного журнала по сложным системам и проекта Wolfram Alpha («база знаний и набор вычислительных алгоритмов»), предложил классификацию клеточных автоматов, выделив четыре категории [Wolfram 1984], [Waldrop 1992: 225–226]:

• Класс I.Системы с набором правил, гарантирующих «Судный день». Они обрекают систему на вымирание через несколько поколений, независимо от первоначальной конфигурации.

• Класс II.Эти системы поживее, но не намного. Любая первоначальная конфигурация быстро вырождается в набор скучных статичных состояний.

• Класс III.Эти системы представляют собой другую крайность: они слишком подвижные. При любой начальной конфигурации они развиваются хаотически и не стабилизируются ни в одном из состояний, оставаясь полностью непредсказуемыми.

• Класс IV.В таких системах наборы правил не приводят к неподвижным, статичным или хаотическим состояниям. Они отличаются подвижностью, в них возникают оригинальные и даже удивительные конфигурации, однако в конечном итоге такие системы стабилизируются.

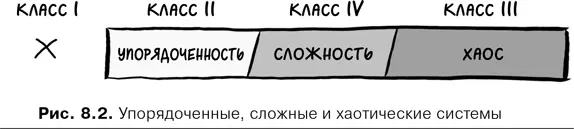
Вас не удивит, что с точки зрения классификации динамических систем классы I и II будут упорядоченными, класс III – хаотическими , а класс IV (знаменитый пример которого – игра «Жизнь») – сложными системами . Если учесть, что сложные системы обычно интерпретируются как те, что находятся между упорядоченностью и хаосом, то системы класса IV должны располагаться между классами II и III (рис. 8.2). (Этот странный способ нумерации делает «базу знаний» Вольфрама еще более интересной.)