Вадим Сысоев - Землеустройство

Задача 3. Построение профиля и вычисление уклона.

Картой называется уменьшенное изображение на плоскости всей земной поверхности или значительных участков местности, размеры которых не позволяют пренебречь кривизной Земли.

Получив карту, студент должен определить ее масштаб по подписи внизу листа, т. е. уяснить, чему соответствует на местности один сантиметр (один миллиметр) на карте. С помощью измерителя и приведенного на карте линейного масштаба определить, чему равно расстояние между отдельными пунктами на карте, назначенными преподавателем.

Далее студент переходит к изучению условных знаков.

На картах и планах для обозначения различных объектов и их характеристик применяют картографические условные обозначения.

Чтобы уметь читать карту и планы, надо хорошо разбираться в применяемых на них условных знаках, образно воспринимая по ним вид каждого изображаемого объекта с его типовыми свойствами и характерными особенностями. Твердое усвоение условных знаков достигается не механическим запоминанием всего их разнообразия, а уяснением принципов их построения, уяснением логической связи между их формой (рисунком) и смысловыми значениями.

На российских топографических планах и картах применяют условные обозначения, представляющие собой единую систему, состоящую из условных знаков, цветового их оформления (расцветки), пояснительных подписей и цифровых обозначений.

Основу системы составляют условные знаки и их расцветка, посредством которых на картах наглядно показываются различные объекты местности и их типовые разновидности. Пояснительные же подписи и цифровые обозначения имеют вспомогательное значение, дополняя условные знаки конкретными данными об индивидуальных особенностях изображаемых объектов. Условные знаки по их назначению и свойствам подразделяются на следующие четыре вида: внемасштабные, линейные, площадные и пояснительные.

Внемасштабные условные знаки применяют для изображения объектов, площади которых не выражаются в масштабе карты или плана. По своему очертанию они напоминают внешний вид изображаемых предметов, однако их действительные размеры нельзя определить по карте или плану.

Линейные условные знаки применяют для изображения объектов линейного характера, длина которых выражается в масштабе карты или плана, а ширина изображается с искажением.

Площадные условные знаки применяют для заполнения площадей объектов, выражающихся в масштабе карты или плана и ограничиваемых контурами.

Пояснительные условные знаки применяются для дополнительной характеристики объектов и показа их разновидностей.

С изменением масштаба условные знаки несколько изменяются, но их общее начертание сохраняется. Однако при изображении некоторых предметов местности в более мелких масштабах приходится переходить от масштабных условных знаков к внемасштабным. Например, населенные пункты на картах мелких масштабов изображаются кружками.

Студент должен на листе бумаги размером 20×16 см нарисовать условные знаки. Для этого надо расположить один под другим ряд прямоугольников размером 1×2 см, внутри которых нанести условные знаки и подписать сбоку их название. При зарисовке можно пользоваться специальными плакатами или учебником геодезии (Приложения А, Б).

Географическими координатами точки являются ее долгота и широта. Вначале следует прочесть географические координаты углов карты. На рисунке 1 показана долгота западного меридиана 18°00´, а восточного 18°07´30´´, 54°40´ и 54°45´ – широты параллелей, ограничивающих карту с Юга и Севера.

Для определения географических координат точек на карте нанесена градусная рамка с минутными интервалами, которые через один залиты на половину высоты черным цветом. Определим географические координаты точки А. Для этого из точки А проводим линии, параллельные меридиану, и параллели, ограничивающие карту (рисунок 1).

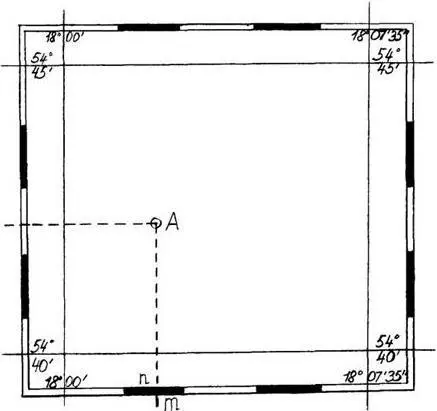
Рисунок 1 – Определение геодезических координат точки

По градусной рамке отсчитываем долготу λ = 18°02´, широту φ = 54°42´30´´.

Число секунд определяется следующим образом. Замеряем длину отрезков m и n в миллиметрах. Как указано выше, отрезок m равен 1 минуте или 60 секунд. Следовательно, одна секунда соответствует мм. Зная длину отрезка n в мм, определяем число секунд X по формуле: