Три семейства картографических проекций
Процесс создания картографической проекции может быть наглядно показан путем помещения источника света внутрь прозрачного глобуса с обозначенными параллелями и меридианами. Свет падает на лист бумаги. Различные способы проецирования имитируются оборачиванием глобуса листом в форме цилиндра, конуса, или просто прикладыванием плоскоголиста. Каждый из этих методов называется семейством картографических проекций. Таким образом, существуют семейства цилиндрических, коническихи плоскостных проекций(см. Рисунок 62 а, б, в).
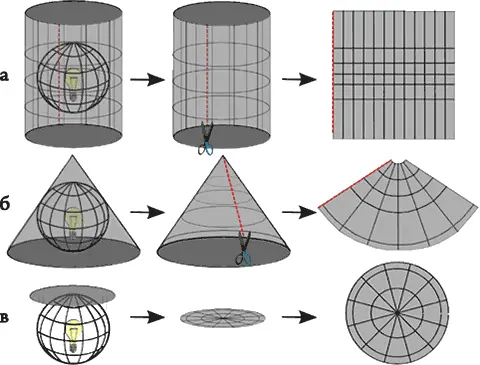
Рисунок 62: Три семейства картографических проекций: а) цилиндрические, б) конические и в) плоскостные проекции.
Процесс проецирования осуществляется с использованием математических принципов геометрии и тригонометрии. Процесс, показанный выше, моделируется числовыми функциями.
Точность картографических проекций
Картографические проекции по определению не могут передать сферическую поверхность со 100% точностью. В ходе проецирования любая карта будет иметь искажения углов, расстоянийили площадей. Картографическая проекция может быть компромиссной, т. е. искажать все три свойства в некоторых допустимых пределах. Примером компромиссной проекции служит проекция Робинсона(см. Рисунок 63), часто используемая для карт мира.
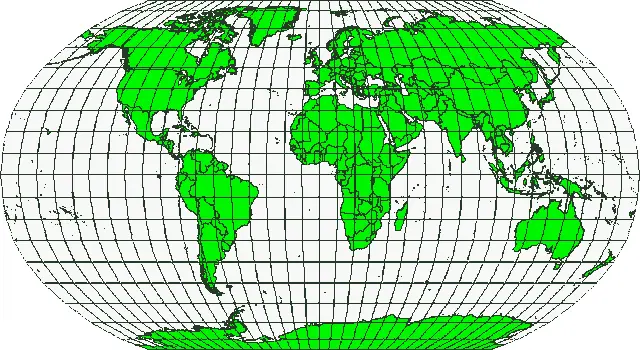
Рисунок 63: Проекция Робинсона является компромиссной проекцией, в которой искажения площадей, углов и расстояний находятся на приемлемом уровне.
Как уже сказано, при перенесении Земли на плоскость сохранить точность всех характеристик одновременно невозможно. Это означает, что если Вам нужно осуществлять точные аналитические операции по карте, Вы должны выбрать картографическую проекцию, которая наилучшим образом сохраняет точность характеристики, которую Вы будете измерять. Например, если Вы хотите измерять расстояния на Вашей карте, Вам следует выбрать проекцию, которая обеспечивает высокую точность расстояний.
Равноугольные картографические проекции
На глобусе главные направления розы ветров (север, запад, юг и восток) всегда находятся под углом 90 градусов друг к другу. Другими словами, меридианы всегда находятся под прямым углом к параллелям. Такие углы могут быть сохраненына картографической проекции, называемой равноугольной. Также такая проекция называется конформной, или ортоморфической.
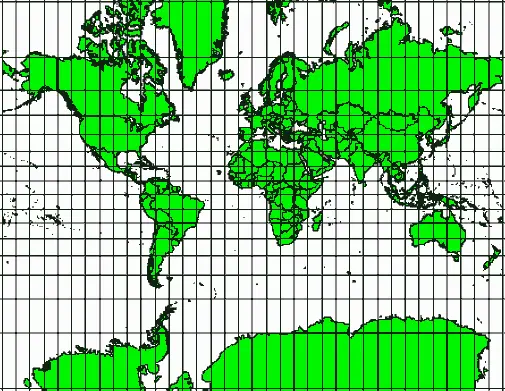
Рисунок 64: Проекция Меркатора используется в случаях, когда важно сохранить углы. В то же время, она сильно искажает площади в высоких широтах.
Подобные проекции используются, когда важно сохранить правильные углы, в частности для навигационных и метеорологических задач. Важно помнить, что сохранение правильных углов на карте ведет к искажению других характеристик и действительно на малых площадях. Так, конформная проекция искажает площади, т. е. если на карте с конформной проекцией будут измерены площади, их значения будут неправильными. Чем больше область, изображенная на карте, тем больше будут искажены площади. Примеры конформных проекций — Проекция Меркатора(см. Рисунок 64) и Конформная Коническая Проекция Ламберта. Подобные проекции используются на многих картах Геологической Службы США.
Равнопромежуточные проекции
Если Вы хотите правильно измерять расстояния, Вам потребуется картографическая проекция, которая хорошо сохраняет расстояния. Такие проекции, называемые равнопромежуточными, поддерживают постоянный масштаб карты. Карта является равнопромежуточной, когда она корректно отображает расстояния от центра проекции до любой другой точки на карте. Равнопромежуточные проекции обеспечивают правильные расстояния от центра проекции вдоль определенных линий. Эти проекции используются для сейсмического картографирования, а также для задач навигации. Цилиндрическая Проекция Плате-Карре(см. Рисунок 65) и Равнопромежуточная проекцияотносятся к этому типу проекций. Есть и другие проекции, например Азимутальная Равнопромежуточная Проекцияиспользуется на эмблеме ООН (см. Рисунок 66).
Читать дальше















