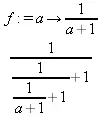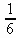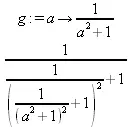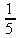Следует отметить, что в математических выражениях операторы имеют общепринятый приоритет , то есть порядок выполнения операторов в сложном выражении. Низшим приоритетом обладают операторы сложения и вычитания. Более высокий приоритет у операторов умножения, деления, затем возведения в степень, выполнения логических операций и так далее. Для изменения приоритета операций в математических выражениях используются круглые скобки. Выражения в скобках выполняются в первую очередь вне зависимости от приоритета входящих в них операций. Степень вложения скобок во всех современных математических системах не ограничивается.
Понятие приоритета облегчает однозначную интерпретацию математических выражений. К примеру, в выражении 2+3*5 вначале будет вычислено 3*5, а затем к результату прибавится 2. В итоге будет вычислено значение 17. А в выражении (2+3)*5 вначале будет вычислено выражение в скобках (2+3), затем оно будет умножено на 5, так что результат будет 25. Таким образом скобки позволяют менять приоритет операций. Степень вложения скобок в современных системах компьютерной математики не ограничена. Однако иногда применение лишних скобок может повлиять на выбор правил вычисления выражений, например при вычислении степеней.
Формально операторы представлены своими идентификаторами в виде специальных математических знаков, слов и иных имен. Операторы, как это вытекает из их названия, обеспечивают определенные операции над данными, представленными операндами. Имеется пять основных типов операторов:
• binary — бинарные операторы (двумя операндами);
• unary — унарные операторы (с одним операндом);
• nullary — нуль-арные операторы (без операнда — это одна, две и три пары кавычек);
• precedence — операторы старшинства (включая логические операторы);
• functional — функциональные операторы.
Для просмотра операторов и их свойств можно использовать следующие команды вида:
> ?operators[вид];
где вид — название вида оператора, указанное выше. Будет выведена страница справки по операторам заданного вида. А для изучения примеров применения операторов нужно задать и исполнить команду
> ?operators[examples];
Команда
> ?define;
позволяет ознакомиться с функций define. С ее помощью можно определять новые операторы.
3.1.3. Применение бинарных (инфиксных) операторов
Бинарные операторы , именуемые также инфиксными , используются с двумя операндами, обычно размещаемыми по обе стороны от оператора. В ядро Maple включено около трех десятков бинарных операторов. Основные из них перечислены в таблице 3.1. Чуть позже мы рассмотрим и другие бинарные операторы. Примеры вычисления выражений с бинарными операторами (файл ор):
> 2+3-(-4);
9
> [2^3,2**3];
[8,8]
> 7 mod 5;
2
> [3@2,3@@2];
[3, 3 (2)]
> [х@х,х@@х];
[x (2), x (x)]
> [х$3,х$4];
[х, x, x, x, x, x, x]
Таблица 3.1. Бинарные операторы
| Обозначение |
Оператор |
Обозначение |
Оператор |
| + |
Сложение |
@ |
Оператор композиции |
| - |
Вычитание |
@@ |
Повторение композиции |
| * |
Умножение |
, |
Разделитель выражений |
| / |
Деление |
:= |
Присваивание |
| ** или ^ |
Возведение в степень |
.. |
Задание интервала |
| mod |
Остаток от деления |
, |
Разделитель выражений |
| $ |
Оператор последовательности |
&* |
Некоммутативное умножение |
| . |
Разделительная точка |
& |
Нейтральный оператор |
| || |
Конкатенация (объединение) |
|
|
> int(х^2,х=1..4);
21
> S: = `Hello` || ` my ` || `friend!`;
S := Hello my friend!
Оператор композиции @@ может использоваться для создания и вычисления сложных функций, содержащих цепные дроби:
> f:=а->1/(1+а);(f@@3)(а);
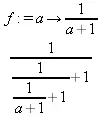
> f(5);
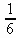
> g:=а->1/(1+а^2);(g@@3)(а);
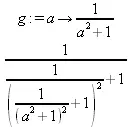
> g(2);
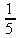
А вот еще один пример применения этого оператора для составления цепного радикала и вычисления ряда таких цепочек в цикле:
Читать дальше
Конец ознакомительного отрывка
Купить книгу