Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Обратите внимание на функцию Int — инертную форму функции int. Как уже отмечалось, инертная форма служит для вывода записи интеграла в естественной математической форме, но с отложенным «на потом» выводом результата вычислений.

Полезно также рассмотреть последний пример. В нем задано выражение, интеграл которого вычисляется с применением контекстного меню правой клавиши мыши. Результатом является переменная R2 со значением интеграла. Контекстное меню демонстрирует также возможность оперативного проведения над заданным выражением множества других символьных операций, которые будут детально описаны в последующих главах книги.

На другом рисунке (рис. 1.26) показано вычисление интеграла, который не имеет представления через функции системы Maple 9.5. но может быть вычислен ею в численном виде.

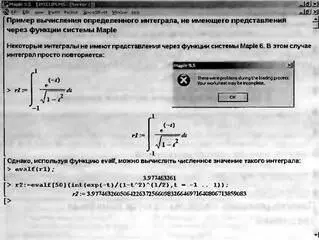
Рис. 1.26. Численное вычисление значения интеграла, не имеющего аналитического представления

На рис. 1.26 представлены два варианта такого вычисления. В первом случае использована функция eval(expr) для вычисления значения заданного выражения expr. Во втором случае используется эта функция в иной нотации, позволяющей получить результат с заданным числом цифр (50 в нашем примере).

Одной из проблем в применении систем компьютерной алгебры является «разбухание » результатов — как оконечных, так и промежуточных. К примеру, численное решение кубического уравнения не вызовет трудностей даже на калькуляторе [13, 14, 16], тогда как системы символьной математике выдают его в виде громоздких, хотя и точных формул — см. примеры на рис. 1.27. Заметьте, что для кубического уравнения в окно поместилась только небольшая часть решения.

Рис. 1.27. Решение квадратного и кубического уравнений в символьной форме

Просмотреть оставшуюся часть можно с помощью линейки прокрутки в правой части окна документа.

Стремление системы выдать полный и математически предельно точный результат, безусловно, очень важно для математиков. Но для многих прикладных задач, с которыми имеют дело инженеры и техники, она оборачивается большими неудобствами. Инженеры часто прекрасно знают, какие из членов математических формул можно отбросить, тогда как для математика-теоретика или аналитика такое действо — типичное кощунство.

Приведем еще один характерный пример — решение системы линейных уравнений с помощью функции solve (рис. 1.28). Обратите внимание на форму задания уравнений и выдачи результатов и поразительную естественность решения задачи. Значение переменной z на рис. 1.28 выделено, при этом видно, что Maple отображает его поле под панелью инструментов.

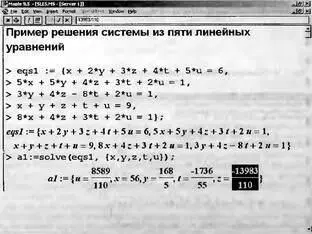
Рис. 1.28. Решение системы из пяти линейных уравнений

Maple стремится выдать результат с максимальной точностью — обычно в форме рациональных чисел. Но с помощью функции evalf можно получить результат в форме вещественных чисел в формате с плавающей точкой.

Слова solve, diff, int и evalf с их аргументами являются именами встроенных в систему функций, возвращающих символьные значения результатов. В общих чертах назначение их уже вполне понятно. Но в последующих главах книги мы познакомимся с этими и многими функциями гораздо более подробно и обстоятельно.

Для многих пользователей (особенно начинающих) при работе с Maple 9.5 удобно работать с панелями инструментов , которые находятся прямо под строкой меню. На рис. 1.29 показано назначение кнопок панели инструментов (Tool Bar). Эти кнопки дублируют наиболее важные операции главного меню и имеют наглядные и типовые для Windows-приложений обозначения. Назначение кнопок и других деталей интерфейса также показаны на рис. 1.29.

Рис. 1.29. Панель инструментов

При необходимости панели инструментов можно убрать с помощью команд меню View. Если графика выводится в отдельное окно, там имеется своя панель инструментов, которое будет описана ниже.