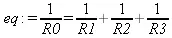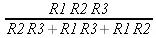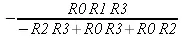Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Если установить указатель мыши на входной ячейке, то это меню будет содержать три важные команды:

Standard Math — включает и выключает показ входных выражений в естественной математической форме;

Maple Input — управляет видом ячейки ввода (математический/текстовый);

Execute — включает выполнение ячейки.

Также, в зависимости от состояния буфера обмена и наличия выделения, в контекстном меню могут присутствовать команды Cut, Сору и Paste.

Левая кнопка мыши может использоваться для передачи фокуса или переноса маркера ввода, а также выделения частей документа.

На рис. 1.20 показан ряд простых вычислений. Среди них задание функции пользователя f(x) с одним параметром х. Нетрудно заметить, что параметр указывается в скобках после имени функции, а для записи выражения функции используется знак присваивания := (двоеточие со знаком равенства). Это старый способ задания функции пользователя, который (что видно из приведенного примера) еще работает, но уже не рекомендуется к применению.

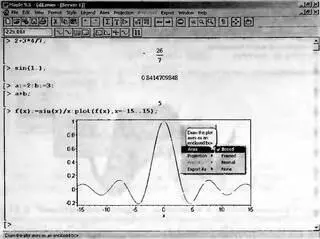
Рис. 1.20. Примеры простых вычислений с построением графика функции пользователя одной переменной

Для построения графика функции f(x) одной переменной используется функция plot в форме

plot(f(x), X = -15..15);

Нетрудно заметить, что при наличии нескольких параметров функции (в нашем случае их два) они разделяются запятыми. Выражение х=-15..15 задает, во-первых, указание, относительно какой переменной строится график, а во-вторых, говорит, в какой области значений меняются значения этой переменной — в нашем случае от -15 до +15. Шаг изменения переменной выбирается автоматически, в зависимости от размеров и вида графика.

Столь же просто, как и график обычной функции в декартовой системе координат, можно построить график трехмерной поверхности. Это показано на примере рис. 1.21. В данном случае задана функция двух переменных z(x,y) в рекомендуемом виде — z:=(x,y)->sin(x*y) и ее график строится с использованием графической функции plot3d. Правила задания пределов изменения переменных х и у соответствуют описанным выше. В данном случае можно было бы задать функцию пользователя и по старинке в виде z(x,y):=sin(x*y).

При выделении графика щелчком левой клавиши мыши на нем график обрамляется рамкой с местами ввода, за которые можно цепляться курсором мыши и растягивать график в ту или иную сторону. Кроме того, мышью при нажатой левой клавише можно вращать график в ту или иную сторону. Ряд возможностей форматирования графика дает контекстное меню правой клавиши мыши, показанное на рис. 1.21. С ними нетрудно разобраться самостоятельно.

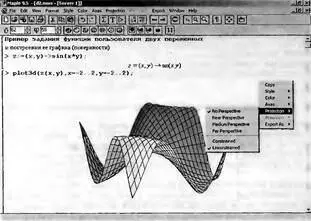
Рис. 1.21. Построение графика трехмерной поверхности, заданной функцией пользователя

Возможно, многих читателей вполне удовлетворят уже описанные возможности, но сила системы Maple 9.5 прежде всего в возможности выполнения аналитических (символьных) вычислений. Поэтому мы перейдем обсуждению некоторых из них.

Maple 9.5, как и другие СКА, открывает обширные возможности выполнения символьных ( аналитических ) вычислений. Мы уже описывали примеры решения квадратного уравнения. Возьмем еще один простой пример — требуется найти сопротивление трех параллельно включенных резисторов R1, R2 и R3 произвольной величины. Из курса электротехники известно, что можно задать следующее равенство, определяющее суммарное сопротивление R0.

> eq:=1/R0=1/R1+1/R2+1/R3;

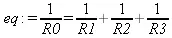
Теперь достаточно использовать функцию решения уравнений solve, чтобы найти значение R0 в общей аналитической форме:

> solve(eq,R0);

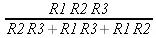
С таким же успехом мы можем найти аналитическое выражение для R1, определяющее R1 через R0, R2 и R3:

> solve(eq,R1);

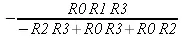
Нетрудно проверить, что результат может быть получен и в численном виде для конкретных значений R1, R2 и R3 :