Энтони Уильямс - Параллельное программирование на С++ в действии. Практика разработки многопоточных программ

Атомарная переменная go (2)служит для того, чтобы все потоки начали работу по возможности одновременно. Запуск потока — накладная операция и, не будь явной задержки, первый поток мог бы завершиться еще до того, как последний зачал работать. Каждый поток ждет, пока переменная goстанет равна true, и только потом входит в главный цикл (3), (5), а переменная goустанавливается в trueтолько после запуска всех потоков (6).

Ниже показан один из возможных результатов прогона этой прогона:

(0,0,0),(1,0,0),(2,0,0),(3,0,0),(4,0,0),(5,7,0),(6,7,8),(7,9,8),(8,9,8),(9,9,10)

(0,0,0),(0,1,0),(0,2,0),(1,3,5),(8,4,5),(8,5,5),(8,6,6),(8,7,9),(10,8,9),(10,9,10)

(0,0,0),(0,0,1),(0,0,2),(0,0,3),(0,0,4),(0,0,5),(0,0,6),(0,0,7),(0,0,8),(0,0,9)

(1,3,0),(2,3,0),(2,4,1),(3,6,4),(3,9,5),(5,10,6),(5,10,8),(5,10,10),(9,10,10),(10,10,10)

(0,0,0),(0,0,0),(0,0,0),(6,3,7),(6,5,7),(7,7,7),(7,8,7),(8,8,7),(8,8,9),(8,8,9)

Первые три строки относятся к потокам, выполнявшим обновление, последние две — к потокам, которые занимались только чтением. Каждая тройка — это значения переменных x, y, zв порядке итераций цикла. Следует отметить несколько моментов.

• В первом наборе значения xувеличиваются на 1 в каждой тройке, во втором наборе на 1 увеличиваются значения y, а в третьем — значения z.

• Значения x(а равно yи z) увеличиваются только в пределах данного набора, но приращения неравномерны и относительный порядок в разных наборах различен.

• Поток 3 не видит обновлений xи y, ему видны только обновления z. Но это не мешает другим потокам видеть обновления zнаряду с обновлениями xи y.

Это всего лишь один из возможных результатов выполнения ослабленных операций. Вообще говоря, возможен любой результат, в котором каждая из трех переменных принимает значения от 0 до 10, и в каждом потоке, обновляющем некоторую переменную, ее значения монотонно изменяются от 0 до 9.

Чтобы попять, как всё это работает, представьте, что каждая переменная — человек с блокнотом, сидящий в отдельном боксе. В блокноте записана последовательность значений. Вы можете позвонить сидельцу и попросить либо прочитать вслух какое-нибудь значение, либо записать новое. Новое значение он записывает в конец последовательности.

При первой просьбе дать значение человек может прочитать любое значение из списка, имеющегося в данный момент. В ответ на следующую просьбу он может прочитать либо то же самое значение, либо значение, расположенное позже него в списке, но никогда — значение, расположенное раньше уже прочитанного. Если вы просили записать значение, а потом прочитать, то он может сообщить либо значение, записанное в ответ на вашу просьбу, либо расположенное позже него в списке.

Теперь представьте, что в начале списка находятся значения 5, 10, 23, 3, 1, 2. Человек может прочитать любое из них. Если он скажет 10, то в следующий раз он может прочитать также 10 или любое последующее число, но не 5. Если вы позвоните пять раз, то может услышать, например, последовательность «10, 10, 1, 2, 2». Если вы попросите записать 42, он добавит это число в конец списка. Если вы затем будете просить прочитать число, то он будет повторять «42», пока в списке не появится новое число и он не захочет назвать его.

Предположим далее, что у Карла тоже есть телефон этого человека. Карл тоже может позволить ему с просьбой либо прочитать, либо записать число. При этом к Карлу применяются те же правила, что и к вам. Телефон только один, поэтому в каждый момент времени человек общается только с одним из вас, так что список в его блокноте растет строго последовательно. Но из того, что вы попросили записать его новое число, вовсе не следует, что он должен сообщить его Карлу. и наоборот. Если Карл попросил назвать число и услышал в ответ «23», то из того, что вы попросили записать число 42, не вытекает, что в следующий раз Карл услышит его. Человек может назвать Карлу любое из чисел 23, 3, 1, 2, 42 или даже 67, если после вас позвонил Фред и попросил записать это число. Он даже может назвать Карлу последовательность «23, 3, 3, 1, 67», и это не будет противоречить тому, что услышали вы. Можно представить себе, что человек запоминает, какое число кому назвал, сдвигая указатели, на которых написано имя спрашивающего, как показано на рис. 5.5.

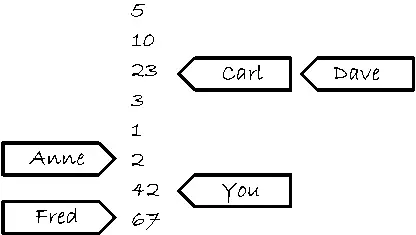
Рис. 5.5.Блокнот человека, сидящего в боксе