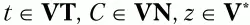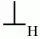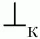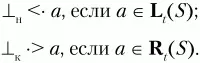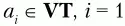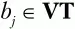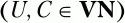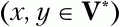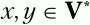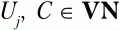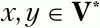Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

3. Если на предыдущем шаге хотя бы одно множество L(U) или R(U) для некоторого символа грамматики изменилось, то надо вернуться к шагу 2, иначе – построение закончено.

Для нахождения множеств L t(U) и R t(U) используется следующий алгоритм:

1. Для каждого нетерминального символа грамматики U строятся множества L(U) и R(U).

2. Для каждого нетерминального символа грамматики U ищутся правила вида U → tz и U → Ctz, где

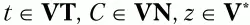
терминальные символы t включаются во множество L t(U). Аналогично для множества R t(U) ищутся правила вида U → zt и U → ztC (то есть во множество L t(U) записываются все крайние слева терминальные символы из правых частей правил для символа U, а во множество R t(U) – все крайние справа терминальные символы этих правил). Не исключено, что один и тот же терминальный символ будет записан в оба множества – L t(U) и R t(U).

3. Просматривается множество L(U), в которое входят символы U', U' … Множество L t(U) дополняется терминальными символами, входящими в L t(U'), L t(U')… и не входящими в L t(U). Аналогичная операция выполняется и для множества R t(U) на основе множества R(U).

Для практического использования матрицу предшествования дополняют терминальными символами

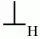
и

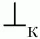
(начало и конец цепочки). Для них определены следующие отношения предшествования:

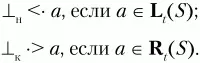
Имея построенные множества L t(U) и R t(U), заполнение матрицы операторного предшествования для КС-грамматики G(VT,VN,P,S) можно выполнить по следующему алгоритму:

1. Берем первый символ из множества терминальных символов грамматики VT:

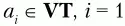
Будем считать этот символ текущим терминальным символом.

2. Во всем множестве правил Р ищем правила вида C → xa iby или C → xa iUb jy, где а i– текущий терминальный символ, Ь j – произвольный терминальный символ

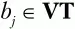
U и С – произвольные нетерминальные символы

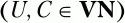
а х и у – произвольные цепочки символов, возможно пустые

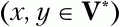
Фактически производится поиск таких правил, в которых в правой части символы а iи Ъ jстоят рядом или же между ними есть не более одного нетерминального символа (причем символ а iобязательно стоит слева от Ь j).

3. Для всех символов Ь j, найденных на шаге 2, выполняем следующее: ставим знак «=.» («составляет основу») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом а i, и столбца, помеченного символом b j.

4. Во всем множестве правил Р ищем правила вида С → xa iU jy, где а i– текущий терминальный символ, U jи С– произвольные нетерминальные символы (U j,

а х и у – произвольные цепочки символов, возможно пустые

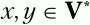
Фактически ищем правила, в которых в правой части символ а iстоит слева от нетерминального символа U j.

5. Для всех символов U j, найденных на шаге 4, берем множество символов L t(U j). Для всех терминальных символов c k, входящих в это множество, выполняем следующее: ставим знак «<.» («предшествует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом a i, и столбца, помеченного символом с k.

6. Во всем множестве правил Р ищем правила вида С → xU ja iy, где a i– текущий терминальный символ, U jи С – произвольные нетерминальные символы

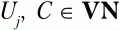
а x и y – произвольные цепочки символов, возможно пустые

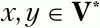
Фактически ищем правила, в которых в правой части символ а стоит справа от нетерминального символа U j.