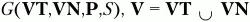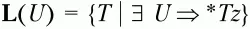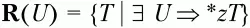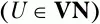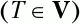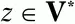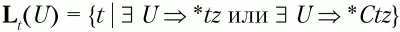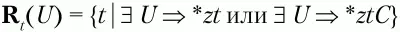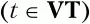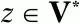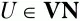Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

На основании отношений предшествования строят матрицу предшествования грамматики. Строки матрицы предшествования помечаются первыми (левыми) символами, столбцы – вторыми (правыми) символами отношений предшествования. В клетки матрицы на пересечении соответствующих столбца и строки помещаются знаки отношений. При этом пустые клетки матрицы говорят о том, что между данными символами нет ни одного отношения предшествования.

Существует несколько видов грамматик предшествования. Они различаются по тому, какие отношения предшествования в них определены и между какими типами символов (терминальными или нетерминальными) могут быть установлены эти отношения. Кроме того, возможны незначительные модификации функционирования самого алгоритма «сдвиг-свертка» в распознавателях для таких грамматик (в основном на этапе выбора правила для выполнения свертки, когда возможны неоднозначности) [1].

Выделяют следующие виды грамматик предшествования:

• простого предшествования;

• расширенного предшествования;

• слабого предшествования;

• смешанной стратегии предшествования;

• операторного предшествования.

Далее будут рассмотрены ограничения на структуру правил и алгоритмы разбора для грамматик операторного предшествования.

Матрицу операторного предшествования КС-грамматики можно построить, опираясь непосредственно на определения отношений предшествования [1, 3, 7], но проще и удобнее воспользоваться двумя дополнительными типами множеств – множествами крайних левых и крайних правых символов, а также множествами крайних левых терминальных и крайних правых терминальных символов для всех нетерминальных символов грамматики.

Если имеется КС-грамматика

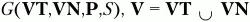
то множества крайних левых и крайних правых символов определяются следующим образом:

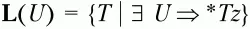
– множество крайних левых символов относительно нетерминального символа U;

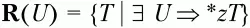
– множество крайних правых символов относительно нетерминального символа U,

где U – заданный нетерминальный символ

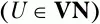
T – любой символ грамматики

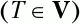
а z – произвольная цепочка символов (

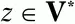
цепочка z может быть и пустой цепочкой).

Множества крайних левых и крайних правых терминальных символов определяются следующим образом:

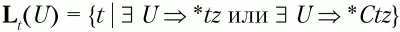
– множество крайних левых терминальных символов относительно нетерминального символа U;

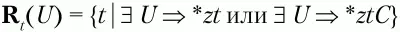
– множество крайних правых терминальных символов относительно нетерминального символа U,

где t – терминальный символ

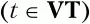
U и С – нетерминальные символы (U,

а z – произвольная цепочка символов (

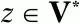
цепочка z может быть и пустой цепочкой).

Множества L(U) и R(U) могут быть построены для каждого нетерминального символа

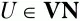
по очень простому алгоритму:

1. Для каждого нетерминального символа U ищем все правила, содержащие U в левой части. Во множество L(U) включаем самый левый символ из правой части правил, а во множество R(U) – самый правый символ из правой части (то есть во множество L(U) записываем все символы, с которых начинаются правила для символа U, а во множество R(U) – символы, которыми эти правила заканчиваются). Если в правой части правила для символа U имеется только один символ, то он должен быть записан в оба множества – L(U) и R(U).

2. Для каждого нетерминального символа U выполняем следующее преобразование: если множество L(U) содержит нетерминальные символы грамматики [U', U', …, то его надо дополнить символами, входящими в соответствующие множества L(U'), L(U')… и не входящими в L(U). Ту же операцию надо выполнить для R(U). Фактически, если какой-то символ U' входит в одно из множеств для символа U, то надо объединить множества для U' и U, а результат записать во множество для символа U.