Тайнан Сильвестр - Геймдизайн. Рецепты успеха лучших компьютерных игр от Super Mario и Doom до Assassin’s Creed и дальше

Другие стратегии в игре «камень, ножницы, бумага» не находятся в равновесии. Например, представьте, что вы должны были выбрать камень в 35 % случаев, а ножницы и бумагу – в 32,5 %. Теперь соперник может победить вас, изменив свою стратегию, выбирая бумагу в 100 % случаев. Если один игрок может выиграть, изменив свою собственную стратегию, это не равновесие Нэша.

Смешанные равновесия легко решить в таких простых играх, как «камень, ножницы, бумага» и «сравнение монет», в которых один игрок сразу выигрывает, а другой проигрывает. Но это необычный случай. В большинстве реальных стратегических взаимодействий разные исходы дают разные результаты. Например, в файтинге блок бьет джеб, не нанося урона, джеб бьет бросок, нанося немного урона, а бросок бьет блок, нанося много урона. Это аналог версии игры в «камень, ножницы, бумагу», где вы получаете 1 доллар, если выигрываете, показав бумагу или ножницы, и 5 долларов, если выигрываете, показав камень. Платежная матрица выглядит так:

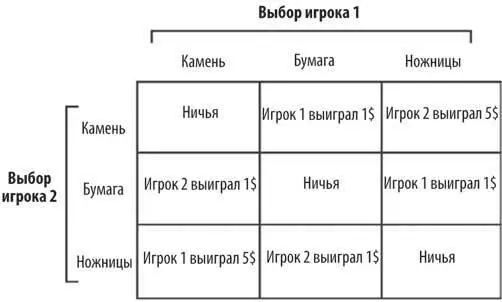
Показывать каждый раз камень и надеяться на 5 долларов – наивная стратегия.

Проблема в том, что это предсказуемо. Противник может показывать только бумагу, и вы уйдете ни с чем. Чтобы хорошо играть в эту игру, нужна смешанная стратегия, когда вы произвольно выбираете между камнем, бумагой и ножницами. Но вы не можете разыгрывать ходы равномерно, как в классической RPS, иначе соперник начнет просто показывать камень чаще. Так как часто нужно делать каждый ход, чтобы заработать максимум?

Здесь вступает в игру математический аспект теории игр. Учитывая стратегическое взаимодействие и выигрыши, специалисты по теории игр могут рассчитать точное соотношение в смешанной стратегии, которое образует равновесие Нэша. Геймдизайнерам не нужно делать количественный анализ, но важно понять соотношение, поэтому я продемонстрирую это на реальном примере.

В футболе при пенальти мяч летит со скоростью до 55 м/с. На этой скорости мячу требуется примерно одна пятая секунды, чтобы преодолеть расстояние от ноги подающего к цели. Вратарю недостаточно этого времени, чтобы прыгнуть и попытаться не пропустить мяч после того, как по нему уже ударили. Единственный выбор – прыгнуть до удара по мячу. В то же время подающий должен выбрать цель, не зная при этом, куда прыгнет вратарь.

Это игра под названием «сравнение монет». Вратарь хочет не пропустить гол, а подающий, наоборот, забить.

В этой игре платеж подающего – вероятность того, что он забьет гол. Его шансы на выигрыш при правильной блокировке выше при ударе вправо, чем влево, шансы забить без блокировки также выше вправо, чем влево. Конечно, его выигрыш остается лучше при ударе влево и отсутствии блокировки, чем при ударе вправо и наличии блокировки. В остальном удар вправо будет представлять собой чистую стратегию равновесия, которая будет непреднамеренно использоваться постоянно.

Лучшая стратегия для подающего – произвольно чередовать удары вправо и влево в разных пропорциях, в большинстве случаев забивая вправо, иногда разбавляя их офсайдами, чтобы вратарь не расслаблялся. В то же время вратарь должен отражать его, большую часть времени блокируя удары вправо, а иногда и удары влево.

Мы можем вычислить точные пропорции на основании вероятности, с которой футболист забьет для каждой из четырех возможных комбинаций со стороны подающего/стороны вратаря. Однако во время исследований были получены данные о сотнях ударов в играх Европейской лиги, на основании которых составлена следующая таблица процентного соотношения шанса забить гол (которая фактически является платежной матрицей):

Из этих цифр видно, что лучшая стратегия для подающего – забивать в правый угол 59,7 %, а в левый – 40,3 %. Эта смешанная стратегия дает общий шанс успеха на уровне 74,0 % независимо от действий вратаря.

Любое отступление от этого соотношения позволяет вратарю улучшать свои результаты, выбрав чистую стратегию прыжков только вправо или влево. Например, если бы подающий забивал вправо 65 % ударов, а не 59,7 %, у него бы только 72,6 % ударов по воротам, при этом вратарь использовал бы свою стратегию прыжков только вправо.

Ключ к смешанному равновесию Нэша в том, что в равновесии каждый возможный ход имеет равный платеж.