Тайнан Сильвестр - Геймдизайн. Рецепты успеха лучших компьютерных игр от Super Mario и Doom до Assassin’s Creed и дальше

Однако вопреки распространенному мнению, треугольник в игре «камень, ножницы, бумага» – не единственная базовая структура дизайна без равновесия Нэша. Вспомните битву за замок. Остается четыре хода, а не три. И у каждого игрока два варианта. Это не похоже на игру в «камень, ножницы, бумага», но, как вы видите, в этом случае равновесия Нэша тоже нет.

Паттерн игры «камень, ножницы, бумага» не образует равновесия Нэша для симметричных игр, в которых игроки ходят одинаково. Но в несимметричных играх, таких как битва за замок, мы используем другой паттерн, названный в честь другой старой игры – «орлянка».

В этой игре один игрок заявляет, что он ищет пару. Игроки не видят монетки друг друга. Каждый игрок кладет монетку орлом или решкой вверх. Затем они одновременно их раскрывают. Если монетки совпали, побеждает игрок, который искал пару. Если нет, побеждает его противник. Это выглядит следующим образом:

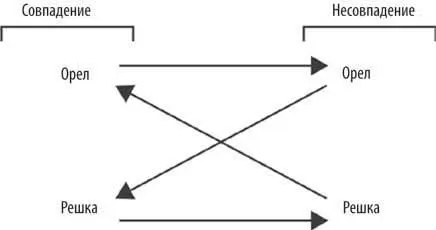
Хотя об этом часто и не говорят, но паттерн «орлянки» постоянно появляется в многопользовательских играх. Битва за замок – это аналогия «орлянки», потому что обороняющийся хочет, чтобы его оборона совпадала с вашим нападением, а вы хотите обратного. В многопользовательском шутере, когда вы защищаете объект в помещении с двумя дверями, вы играете в «сравнение монет»; вы хотите защитить дверь, через которую захочет атаковать соперник, а он, в свою очередь, хочет войти через другую дверь и выстрелить вам в спину. В стратегической игре World War II обороняющийся может решать, тратить ли ресурсы на установку мин, а нападающий может решать, тратить ли ресурсы на то, чтобы добывать тральщики. Вы не хотите расставлять мины, которые будут найдены, и вы также не хотите искать мины, которых нет.

Давайте рассмотрим реальный пример схемы «орлянки» в геймдизайне. В StarCraft II бои между игроками Зергами и Терранами часто ведут четыре юнита: Осадные танки Терранов и Морпехи, а также Гиблинги и Муталиски Зергов. Они взаимодействуют так:

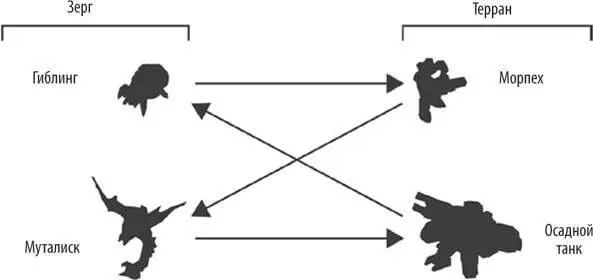
Муталиски летают, поэтому они автоматически поражают Осадные танки, потому что танки не могут стрелять в воздух. Сильнейший урон Морпехов мгновенно разрушает хрупких Муталисков. Гиблинг плавит плотно размещенные группы Морпехов, разбрызгивая кислоту. Но Осадные танки взрывают хрупких Гиблингов с безопасного расстояния. Многие раунды StarCraft II сводятся к повторяющимся взаимодействиям между этими четырьмя юнитами. По сети вы можете проиграть вариации этого паттерна сто часов подряд. Но игра никогда не становится скучной, потому что в ней нет равновесия Нэша, следовательно, у каждого игрока всегда есть возможность выиграть, просчитывая ходы своего противника или сбивая его с толку. Потому что на самом деле смысл игры не в управлении Морпехами и Муталискаими. Речь идет о том, чтобы угадать мысли противника.

«Камень, ножницы, бумага» и «орлянка» – единственные элегантные паттерны дизайна для стратегических взаимодействий – «камень, ножницы, бумага» для симметричных игр, а «сравнение монет» – для асимметричных. Любая альтернатива это не более чем бессмысленное нагромождение новых стратегий.

Например, в игре «камень-бумага-ножницы-ящерица-Спок» каждый символ бьет два других:

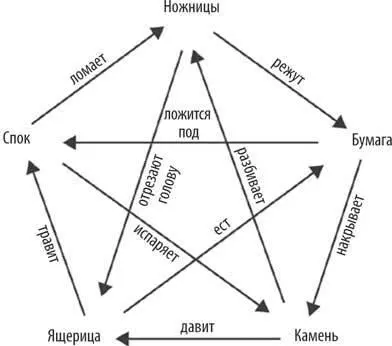
Но RPSLS («камень-бумага-ножницы-ящерица-Спок») ничего не выигрывает с точки зрения интереса к решению в RPS («камень, ножницы, бумага»). Если равновесия Нэша нет, то его нет. Дополнительные символы никак не улучшают интеллектуальную игру предвкушения и хитрости. Дополнительные варианты могут сделать сюжет более интересным, но, скорее всего, это не стоит дополнительного бремени обучения.

Смешанные стратегии

До сих пор я говорил о том, что в таких играх, как «камень, ножницы, бумага», нет равновесия Нэша. Это было не совсем точно. В этой игре нет чистого равновесия Нэша. Но зато существует смешанное.

СМЕШАННОЕ РАВНОВЕСИЕ НЭША – это равновесие Нэша, где каждый игрок произвольным образом выбирает из набора стратегий с некоторым заданным набором вероятностей.

Например, в игре «камень, ножницы, бумага» нет чистого равновесия Нэша, но есть одно смешанное. Игра предполагает, что оба игрока будут показывать каждый ход в 33,3 % случаев. Это равновесие Нэша, поскольку один игрок не может выиграть, отступив от этой схемы (поскольку если соперник показывает по чистой случайности, ваш ход не имеет значения, вы всегда выигрываете половину).