Кубические кривые Безье задаются следующей формулой:
P(t) = А(1-t)³ + 3Bt(1-t)² + 3Ct²(1-t)+Dt³ (1)
где А — начало кривой, D — ее конец, а В и С — первая и вторая опорные точки. Прямая АВ касательная к кривой в точке А , прямая CD — в точке D . Параметр t изменяется от 0 до 1. При t = 0 P(t) = А , при t = 1 P(t) = D.
Одним из важнейших свойств кривой Безье является ее делимость. Если кривую разделить на две кривых в точке t = 0,5, каждая из полученных кривых также будет являться кривой Безье. На этом свойстве основывается алгоритм рисования кривых Безье: если кривая может быть достаточно точно аппроксимирована прямой, рисуется отрезок прямой, если нет — она разбивается на две кривых Безье, к каждой из которых вновь применяется этот алгоритм. Для рисования кривых Безье служат функции PolyBezier, PolyBezierToи PolyDraw.
В некоторых случаях удобно строить кривую Безье не по опорным точкам, а по точкам, через которые она должна пройти. Пусть кривая начинается в точке А, при t =⅓ проходит через точку В' , при t =⅔ — через точку С' , и заканчивается в точке D. Подставляя эти точки в уравнение (1), получаем систему, связывающую В' и С' с В и С . Решая систему, получаем
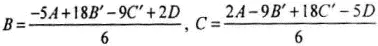 (2)
(2)
Из этих уравнений, в частности, следует, что для любых четырех точек плоскости существует, и притом единственная, кривая Безье, которая начинается в первой точке, проходит при t =⅓ через вторую точку, при t =⅔ — через третью и завершается в четвертой точке. Аналогичным образом можно вычислить опорные точки для кривой, которая должна проходить через заданные точки при других значениях t .
API Windows реализует поддержку специфических объектов, называемых траекториями (path). Траектория представляет собой запись движения пера и включает один или несколько замкнутых контуров. Каждый контур состоит из отрезков прямых и кривых Безье. Для построения траектории в Windows NT/2000/XP могут быть задействованы все графические функции рисования прямых, кривых и замкнутых контуров, а также функции вывода текста (в этом случае замкнутые контуры будут совпадать с контурами символов). В Windows 9x/Me могут быть использованы только функции рисования прямых, ломаных, многоугольников (за исключением PolyDrawи Rectangle), кривых Безье и функций вывода текста. Функции рисования эллипсов, окружностей и эллиптических дуг не могут быть использованы для создания траектории в Windows 9x/Me, т.к. в этих системах эллиптические кривые рисуются специальным алгоритмом, а не аппроксимируются кривыми Безье. Для создания траектории предусмотрены функции BeginPathи EndPath. Все вызовы графических функций, расположенные между BeginPathи EndPath, вместо вывода в контекст устройства будут создавать в нем траекторию.
После того как траектория построена, ее можно отобразить или преобразовать. Мы не будем здесь перечислять все возможные операции с траекториями, остановимся только на преобразовании траектории в ломаную. Как уже отмечалось, все контуры траектории представляют собой набор отрезков прямых и кривых Безье. С другой стороны, при построении кривой Безье она аппроксимируется ломаной. Следовательно, вся траектория может быть аппроксимирована набором отрезков прямой. Функция FlattenPathпреобразует кривые Безье, входящие в состав траектории, в ломаные линии. Таким образом, после вызова этой функции траектория будет состоять из отрезков прямой.
Отметим также некоторые другие преобразование траектории, полезные для создания графических редакторов и подобных им программ. Функция PathToRegionпозволяет преобразовать траекторию в регион. Это может понадобиться, в частности, при определении того обстоятельства, попадает ли курсор мыши в область объекта, представляемого сложной фигурой. Функция WidenPathпревращает каждый контур траектории в два контура — внутренний и внешний. Расстояние между ними определяется толщиной текущего пера. Таким образом, траектория как бы утолщается. После преобразования утолщенной траектории в регион можно определить, попадает ли курсор мыши на кривую с учетом погрешности, определяемой толщиной пера.
Получить информацию о точках текущей траектории можно с помощью функции GetPath. Для каждой точки траектории эта функция возвращает координаты и тип точки (начальная линии, замыкающая точка отрезка, точка кривой Безье, конец контура).
Читать дальше
Конец ознакомительного отрывка
Купить книгу

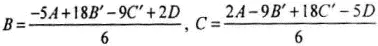 (2)
(2)








