Иван Братко - Программирование на языке Пролог для искусственного интеллекта

Подведем итоги:

• И/ИЛИ-представление основано на философии сведения задач к подзадачам.

• Вершины И/ИЛИ-графа соответствуют задачам; связи между вершинами — отношениям между задачами.

• Вершина, из которой выходят ИЛИ-связи, называется ИЛИ-вершиной. Для того, чтобы решить соответствующую задачу, нужно решить одну из ее задач-преемников.

• Вершина, из которой выходят И-связи, называется И-вершиной. Для того, чтобы решить соответствующую задачу, нужно решить все ее задачи-преемники.

• При заданном И/ИЛИ-графе конкретная задача специфицируется заданием

стартовой вершины и

целевого условия для распознавания

целевых вершин.

• Целевые вершины (или "терминальные вершины") соответствуют тривиальным (или "примитивным") задачам.

• Решение представляется в виде решающего графа — подграфа всего И/ИЛИ-графа.

• Представление задач в форме пространства состояний можно рассматривать как специальный частный случай И/ИЛИ-представления, когда все вершины И/ИЛИ-графа являются ИЛИ-вершинами.

• И/ИЛИ-представление имеет преимущество в том случае, когда вершинами, находящимися в отношении И, представлены подзадачи, которые можно решать независимо друг от друга. Критерий независимости можно несколько ослабить, а именно потребовать, чтобы существовал такой порядок решения И-задач, при котором решение более "ранних" подзадач не разрушалось бы при решении более "поздних" под задач.

• Дугам или вершинам, или и тем, и другим можно приписать стоимости с целью получить возможность сформулировать критерий оптимальности решения.

Для задачи отыскания кратчайшего маршрута (рис. 13.1) И/ИЛИ-граф вместе с функцией стоимости можно определить следующим образом:

• ИЛИ-вершины представляются в форме X-Z, что означает: найти кратчайший путь из X в Z.

• И-вершины имеют вид

X-Z через Y

что означает: найти кратчайший путь из X в Z, проходящий через Y.

• Вершина X-Z является целевой вершиной (примитивной задачей), если на карте существует непосредственная связь между X и Z.

• Стоимость каждой целевой вершины X-Z равна расстоянию, которое необходимо преодолеть по дороге, соединяющей X с Z.

• Стоимость всех остальных (нетерминальных) вершин равна 0.

Стоимость решающего графа равна сумме стоимостей всех его вершин (в нашем случае это просто сумма стоимостей всех терминальных вершин). В задаче рис. 13.1 стартовая вершина — это а-z . На рис. 13.5 показан решающий граф, имеющий стоимость 9. Это дерево соответствует пути [a, b, d, f, i, z], который можно построить, если пройти по всем листьям решающего дерева слева направо.

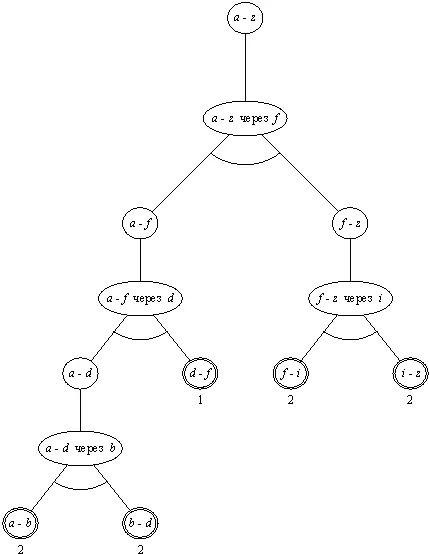
Рис. 13.5. Решающее дерево минимальной стоимости для задачи поиска маршрута рис. 13.1, сформулированной в терминах И/ИЛИ-графа.

Задача о ханойской башне (рис. 13.6) — это еще один классический пример эффективного применения метода разбиения задачи на подзадачи и построения И / ИЛИ-графа. Для простоты мы рассмотрим упрощенную версию этой задачи, когда в ней участвует только три диска:

Имеется три колышка 1, 2 и 3 и три диска а , b и с ( а — наименьший из них, а с — наибольший). Первоначально все диски находятся на колышке 1. Задача состоит в том, чтобы переложить все диски на колышек 3. На каждом шагу можно перекладывать только один диск, причем никогда нельзя помещать больший диск на меньший.

Эту задачу можно рассматривать как задачу достижения следующих трех целей:

(1) Диск а — на колышек 3.

(2) Диск b — на колышек 3.

(3) Диск с — на колышек 3.

Беда в том, что эти цели не независимы. Например, можно сразу переложить диск а на колышек 3, и первая цель будет достигнута. Но тогда две другие цели станут недостижимыми (если только мы не отменим первое наше действие). К счастью, существует такой удобный порядок достижения этих целей, из которого можно легко вывести искомое решение.

Рис. 13.6. Задача о ханойской башне

Порядок этот можно установить при помощи следующего рассуждения: самая трудная цель — это цель 3 (диск с — на колышек 3), потому что на диск c наложено больше всего ограничений. В подобных ситуациях часто срабатывает хорошая идея: пытаться достичь первой самую трудную цель. Этот принцип основан на следующей логике: поскольку другие цели достигнуть легче (на них меньше ограничений), можно надеяться на то, что их достижение возможно без отмены действий на достижение самой трудной цели.