Тимур Машнин - Объектно-ориентированное программирование на Java. Платформа Java SE

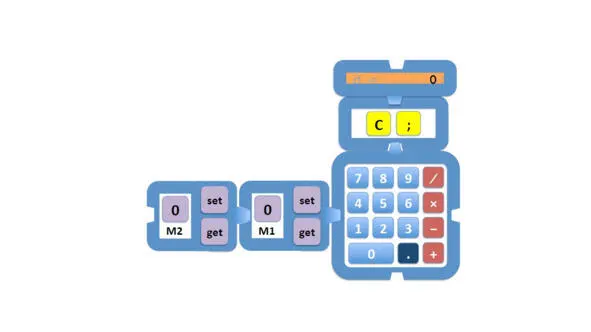
Функция запоминания позволяет нам сохранить значение для будущего использования.

Память может содержать значение, и могут быть связанные с ней операции, такие как MS, чтобы сохранить значение, и MR, чтобы восстановить его или вызвать его.

Иногда есть третья клавиша, MC для очистки памяти,

Назовем эти две клавиши для работы с памятью set и get.

Сейчас ячейки памяти названы предопределенными именами, M1, M2 и т. д.

Но мы хотели бы назвать их x и y, как мы привыкли в математике.

И мы будем присваивать этим ячейкам памяти имена переменных.

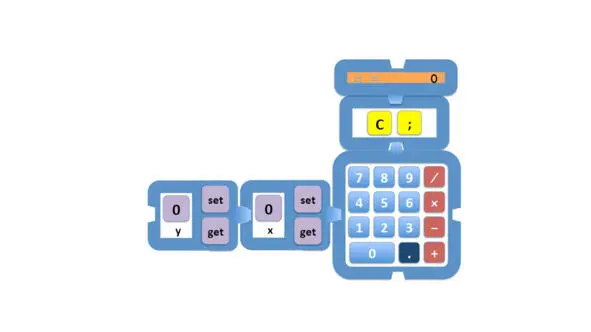
Теперь мы обсудим, что такое начальное значение переменной, которое сохраняется до того, как мы установим переменную в другое значение.

Мы можем сказать, что значение переменной неопределенно.

Поэтому, если мы попытаемся получить это значение, мы получим ошибку.

В калькуляторах, где есть числовые переменные, эта переменная обычно устанавливается равной 0, чтобы избежать ошибки.

Теперь мы хотим, чтобы дисплей показывал что-то, когда мы нажимаем кнопки Set или Get.

Давайте сначала поговорим о Set.

Предположим, что дисплей показывает число 3, и что мы нажимаем кнопку set переменной x.

Теперь значение 3 будет храниться в переменной x.

И дисплей может показать что-то вроде x равно 3 точка с запятой,

Чтобы записать то, что мы только что сделали.

Мы говорим, что мы назначили значение 3 переменной X, и записали это как x равно 3 в инструкции присваивания.

Как только мы установили значение переменной, мы можем использовать это значение в выражениях.

Например, представьте, что у нас есть 5 на дисплее,

И мы хотим добавить значение x.

Мы нажимаем символ плюса, а затем кнопку Get х.

Таким образом, мы увидим на дисплее 5 плюс x.

Но это выражение, и до того, как мы используем оператор присваивания, что дисплей действительно отображает, выражение или законченную операцию?

Мы можем рассматривать выражения в калькуляторе как законченные операции, считая, что дисплей также может считаться переменной, переменной с прямым вводом.

Поэтому на дисплее написано d равно перед выражением.

Таким образом мы преобразуем выражение в операцию.

На слайде показаны различные выражения присваивания.

Здесь показано, что выражения могут также иметь переменные.

И для вычисления выражения, нам нужно найти сохраненное значение в соответствующих переменных.

Теперь может оказаться, что одна и та же переменная появляется как слева, так и справа от присваивания.

Давайте проанализируем это более подробно.

Но сначала, давайте вспомним, что выражение присваивания состоит из переменной, за которой следует символ равенства, за которым следует выражение для вычисления, которое завершается точкой с запятой.

Представьте, что мы имеем три переменные x, y и z.

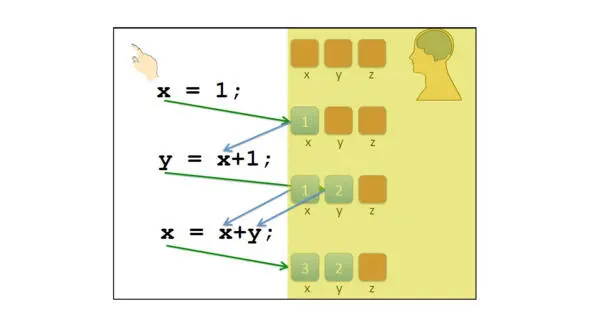
Мы не знаем их начальных значений.

У нас есть первая операция, которая присваивает 1 переменной x.

Поэтому после выполнения содержимое переменной x равно 1.

Следующая операция присваивания y равно x плюс 1.

Сначала мы должны оценить выражение справа, x плюс 1.

Для этого нам нужно получить значение, сохраненное в x.

Поэтому мы получаем 2 и 2 сохраняем в y.

Мы всегда работаем справа налево.

Сначала вычисляем выражение, а затем сохраняем результат в переменной.

Теперь мы сначала получаем значения x и y, складываем их вместе, получаем 3 и сохраняем 3 в x.

Переменные вместе со значениями – это то, что мы называем состоянием.

Таким образом, оператор присваивания преобразует одно состояние в другое состояние.

Здесь состояния обозначены фигурными скобками.

Коллекция значений переменных – это состояние.