Владимир Большаков - КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия

Условие. Точка K лежит на продолжении стороны AD ромба ADCD за точку D, Е — точка пересечения АС и BK (рис. 11.9), AK = 70 мм, точки А, В и Е лежат на окружности диаметра 60 мм, центр которой принадлежит отрезку AK . Найти длину отрезка BK .

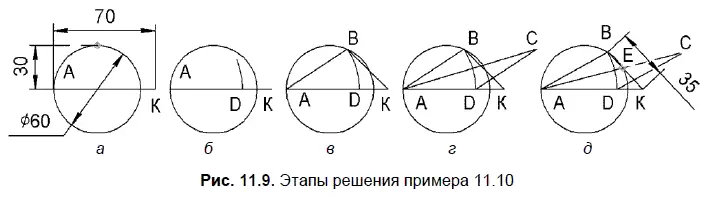
Решение. В данном примере графическое решение получается в результате построения параметрических изображений. Рассмотрим этапы решения примера, показанные на рис. 11.9:

□ а — строится окружность и отрезок заданных размеров. Положение окружности фиксируется привязками к взаимно перпендикулярным отрезкам;

□ б — из точки D проводится дуга с центром в точке А;

□ в — точка дуги В привязкой Точка на кривойперемещается на окружность. Концы отрезков из точек А и K совмещаются с точкой В. В результате точка В может перемещаться по окружности, при этом длины отрезков АВ и KB будут изменяться;

□ г — проводится отрезок DC, параллельный и равный отрезку АВ. Точки пересечения отрезков BK и АС с окружностью еще не совпадают;

□ д — точки пересечения отрезков BK и АС с окружностью объединяются в точке Е, за счет изменения геометрии изображения на рис. 11.10, г . Измеряется длина отрезка BK = 35 мм.

Условие. Трапеция AEFG с основаниями ЕF и AG расположена в квадрате ABCD со стороной 14 так, что точки E, F и G лежат на сторонах AB, BC и CD соответственно (рис. 11.10). Диагонали AF и EG перпендикулярны, а EG = 10√2. Найти периметр трапеции.

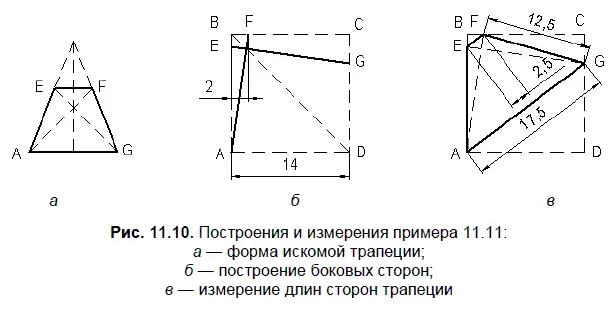
Решение. На рис. 11.10, а показано, что трапеция с взаимно перпендикулярными диагоналями имеет равные по длине боковые стороны, а точка пересечения диагоналей располагается на отрезке, соединяющем середины параллельных сторон трапеции. На рис. 11.10, б выполнены построения по размерам стороны AF и стороны EG, которая симметрична AF относительно отрезка BD, с помощью команды Симметрия. На рис. 11.10, в показаны измеренные длины сторон трапеции, что позволяет найти периметр трапеции, равный 45.

Основной способ решения стереометрических задач — сведение их к планиметрическим. Для этого можно применить метод проекций, заключающийся в проецировании геометрического объекта на подходящую плоскость. Преимуществом метода проекций является то, что он позволяет отобразить на плоском рисунке и увязать друг с другом элементы объектов, не лежащие в одной плоскости. При этом если объект расположить надлежащим образом по отношению к плоскости рисунка, то искомые метрические характеристики (и линейные, и угловые) проецируются на подходящую плоскость в заранее предусмотренном виде, например в натуральную величину.

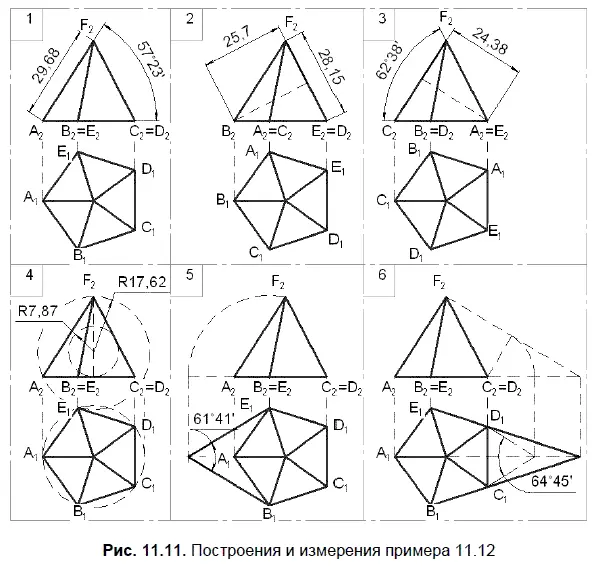
Условие. Дана правильная пятиугольная пирамида ABCDEF. Радиус окружности, описанной вокруг основания АВCDE, равен 16 мм. Высота пирамиды 25 мм. Определить следующие метрические характеристики:

□ длину бокового ребра AF и угол его наклона к основанию;

□ расстояние от вершины В до противоположной грани и высоту этой грани;

□ угол между гранями с общим ребром AF и расстояние от этого ребра до ребра CF ;

□ диаметры вписанной в пирамиду и описанной вокруг пирамиды сфер;

□ угол между ребрами BF и EF, соединяющими вершину пирамиды с противолежащими вершинами основания;

□ угол между боковыми гранями Е = BCF и Q = DEF, не имеющими общего ребра.

Решение примера представлено на рис. 11.11.

Геометрическое тело — часть пространства, ограниченная со всех сторон поверхностью.

Поверхность — это множество всех последовательных положений движущей линии. Эта линия, называемая образующей, при движении может сохранять или изменять свою форму.

Закон перемещения образующей обычно определяется другими линиями, называемыми направляющими, по которым скользит образующая при своем движении.