Жан-Батист Мишель - Неизведанная территория. Как «большие данные» помогают раскрывать тайны прошлого и предсказывать будущее нашей культуры

Оказалось, что этот неожиданный шаг стал решающим. Он позволил им одновременно исправить теорию и шагнуть за ее пределы. Как позднее вспоминал Уилбур Райт, «трудно переоценить важность всей кропотливой работы, которую мы проделали с самодельной аэродинамической трубой. Благодаря данным, которые мы с Орвиллом свели в таблицы, наконец стало возможным создать надежное крыло правильной формы. И как бы знамениты мы ни стали благодаря нашему самолету и его системам контроля, он не был бы возможен без создания аэродинамической трубы и полученным благодаря ей точным аэродинамическим данным».

Оказалось, что благодаря аэродинамической трубе Райтов – довольно простой – удалось измерить массу важных аспектов, улучшающих работу крыла. Братья могли тестировать в своей трубе работоспособность одной конструкции за другой. Получив итоговые данные, они выстроили оптимальную конструкцию крыла и прикрепили ее к самолету. А затем утром 17 декабря 1903 года они вошли в историю.

Если мы хотим понять суть славы, нам тоже нужна аэродинамическая труба.

Многие аспекты славы сложно измерить. Утрату анонимности. Давление, связанное с постоянным вниманием со стороны. Психологические последствия, связанные с угасанием звездного статуса.

Но что можно сказать относительно величины славы – ощущения того, что Иисус более знаменит, чем Леннон, который более знаменит, чем Болдуин, который более знаменит, чем Кобаяси? Важным аспектом величины славы является то, как часто вас упоминают другие люди, в том числе в книгах. А когда речь заходит об упоминаниях людей в книгах, нам на помощь приходят n -грамы.

Разумеется, с помощью n -грамов мы измеряем не славу саму по себе, а упрощение, некое факсимиле славы. Давайте пока что назовем это словом «флава». Нам предстоит ответить на вопрос, достаточно ли четко «флава» отражает подлинную славу, чтобы служить нам в качестве аэродинамической трубы?

Давайте начнем изучение этого вопроса со взгляда на Чарльза Диккенса, одного из самых знаменитых английских писателей. Его первое произведение, «Записки Пиквикского клуба», начиналось в 1836 году как сериал – то есть книга, публиковавшаяся по частям в периодических изданиях. После начала публикации «Записок» 2-грам «Чарльз Диккенс» начинает появляться все чаще. Подобно знаменитому самолету братьев Райт, «флава» Диккенса начала стабильно набирать высоту по мере того, как он последовательно создавал бестселлер за бестселлером, в том числе «Оливера Твиста» (1837), «Рождественскую песнь» (1843), «Дэвида Копперфильда» (1849), «Повесть о двух городах» (1859) и «Большие надежды» (1860). Влияние этих работ на культуру было огромным. Считается, что именно «Рождественская песнь» сделала популярным поздравление «Веселого Рождества», и это вполне соответствует данным n -грамов.

Как и в случае с Дикинсон, смерть Диккенса в 1870 году не привела к угасанию его «флавы». Вместо этого она взвилась до небес, а новости о его уходе из жизни заставили людей вновь восхититься его гением. За несколько десятилетий после смерти частота упоминания его имени достигла пика. Однако к 1900 году 2-грам «Чарльз Диккенс» начал медленное снижение. Несмотря на свою невероятную «популярность» даже в наши дни, интенсивность научного изучения его творчества и включение книг Диккенса в школьную программу, «флава» Диккенса начала плавно угасать в течение последнего столетия.

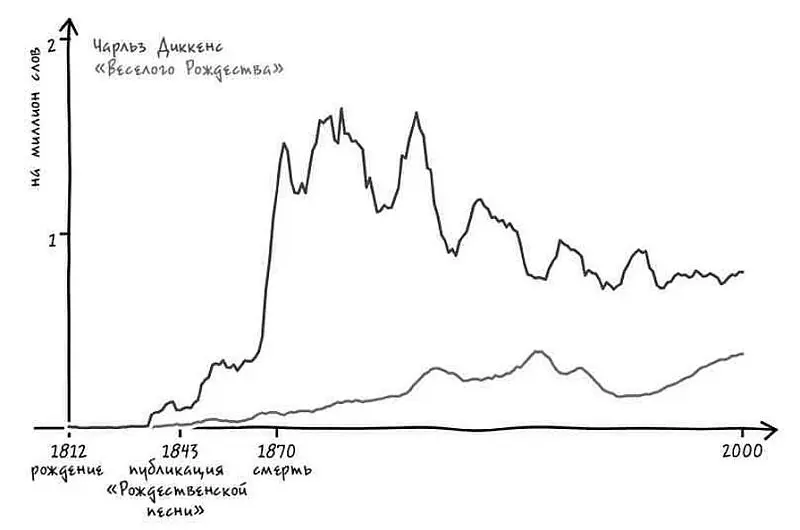
Добавив выражение «Чарльз Диккенс» в нашу аэродинамическую трубу, мы получили интересные результаты, позволяющие вполне точно измерить степень общественного интереса, возникшего к работам Диккенса.

Однако все не так просто. Наш пример также помогает определить расхождения между «флавой», измеренной с помощью книг, и славой, отраженной в наших интуитивных представлениях о культурной важности. Все измерительные приборы допускают ошибку. Чтобы лучше понять происходящее, нужно узнать больше о теории анализа ошибок, хорошо развитой области статистики, изучающей ошибки и проблемы измерений.

Статистики различают два типа ошибок, которые может совершить измерительный прибор. Первый тип называется случайной ошибкой и связан с колебаниями, которые возникают даже в случаях, если объект измерения не меняется. Такие ошибки видны в форме небольших пиков и долин в расчетах «флавы» (несмотря на их частое появление, они порой не имеют никакого смысла). Хорошая новость относительно случайных ошибок заключается в том, что, несмотря на все колебания, значение обычно остается близким к истинному.