Джон Келлехер - Наука о данных. Базовый курс

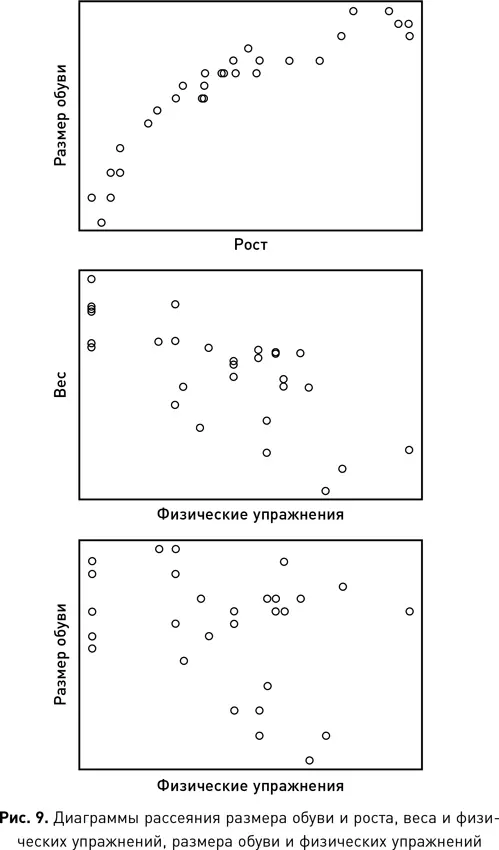
Может показаться, что применение статистического коэффициента корреляции Пирсона к анализу данных ограничено только парами атрибутов. К счастью, мы можем обойти эту проблему, применяя функции для групп атрибутов. В главе 2 мы ввели индекс массы тела (ИМТ) — отношение веса человека (в килограммах) к квадрату его роста (в квадратных метрах). ИМТ был изобретен в XIX в. бельгийским математиком Адольфом Кетле для того, чтобы задать значения для каждой из следующих категорий: люди с недостаточным весом, с нормальным, с избыточным или страдающие ожирением. Мы знаем, что вес и рост имеют положительную корреляцию (как правило, кто выше, тот и тяжелее), поэтому, поделив вес на рост, мы можем отслеживать зависимость первого от второго. Есть два аспекта ИМТ, которые представляют интерес для нашего обсуждения корреляции между несколькими атрибутами. Во-первых, ИМТ — это функция, которая принимает ряд атрибутов в качестве входных данных и сопоставляет их с новым значением. По сути, такое отображение создает новый производный атрибут (в отличие от необработанного атрибута) в данных. Во-вторых, поскольку ИМТ человека представляет собой числовое значение, мы можем рассчитать корреляцию между ним и другими атрибутами.

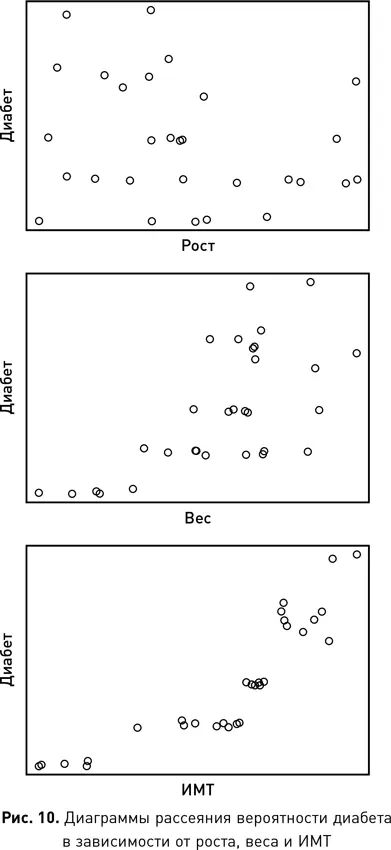
В нашем тематическом исследовании причин развития диабета 2-го типа у белых взрослых американцев мужского пола нам требуется определить, имеет ли какой-нибудь из признаков сильную корреляцию с целевым атрибутом, описывающим вероятность развития диабета у человека. На рис. 10 представлены три диаграммы рассеяния, каждая из которых показывает отношения между целевым атрибутом диабета и одним из следующих признаков (слева направо): ростом, весом и ИМТ. Если посмотреть на диаграмму рассеяния роста и диабета, то в данных не наблюдается какой-либо определенной закономерности, что свидетельствует об отсутствии реальной корреляции между этими двумя атрибутами ( r = –0,277). Средняя диаграмма рассеяния показывает распределение данных для веса и диабета и указывает на положительную корреляцию между людьми с бо́льшей массой тела и вероятностью развития заболевания ( r = 0,655). Нижняя диаграмма рассеяния показывает набор данных, построенный с использованием ИМТ и диабета. Она напоминает среднюю диаграмму, данные так же распределяются снизу слева направо вверх, что указывает на положительную корреляцию. Однако в этой последней диаграмме объекты более тесно связаны, а это означает, что корреляция между ИМТ и диабетом сильнее, чем между диабетом и массой тела. Коэффициент корреляции Пирсона для диабета и ИМТ составляет r = 0,877.

Пример ИМТ иллюстрирует, что можно создать новый производный атрибут, задав функцию, которая принимает несколько атрибутов в качестве входных данных. Таким же путем можно вычислить корреляцию Пирсона между этим производным атрибутом и другим атрибутом в наборе данных. Производный атрибут может иметь более высокую корреляцию с целевым атрибутом, чем любой из отдельно взятых атрибутов, используемых для его генерации. Для лучшего понимания: ИМТ имеет более высокую корреляцию с признаком диабета, чем рост или вес, потому что вероятность развития диабета зависит от взаимосвязи роста и веса, а атрибут ИМТ моделирует именно эту взаимосвязь. Вот почему врачи интересуются ИМТ людей, это дает им больше информации о вероятности развития диабета 2-го типа, чем рост или вес человека по отдельности.

Мы уже отмечали, что выбор атрибутов — ключевая задача в науке о данных. То же касается и моделирования атрибутов. Часто моделирование производного атрибута, который имеет сильную корреляцию с целевым, — это уже полдела в науке о данных. Когда вы знаете правильные атрибуты для представления данных, вы можете создавать модели точно и быстро. Выбор и моделирование правильных производных атрибутов является непростой задачей. ИМТ был разработан в XIX в., однако сейчас алгоритмы машинного обучения способны изучать взаимодействия между входными атрибутами и создавать полезные производные атрибуты, просматривая различные их комбинации, проверяя корреляцию между ними и целевым атрибутом. Вот почему машинное обучение полезно в тех случаях, когда существует множество атрибутов, имеющих слабо выраженную взаимосвязь с процессом, который мы пытаемся понять.