Коллектив Авторов - Базы данных - конспект лекций

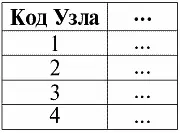
Узлы:

Ссылки:

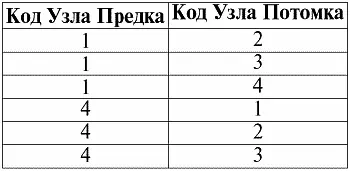
Действительно, вышеприведенное представление исчерпывающе: оно дает всю необходимую информацию для того, чтобы без труда воспроизвести зашифрованную здесь графовую структуру. Например, мы без всяких препятствий можем увидеть, что у узла с кодом «один» имеются три потомка соответственно с кодами «два», «три» и «четыре». Также мы видим, что у узлов с кодами «два» и «три» потомков не имеется вообще, а у узла с кодом «четыре» имеются (также как и у узла «один») три потомка с кодами «один», «два» и «три».

Изобразим граф, заданный классами сущностей, приведенными выше:

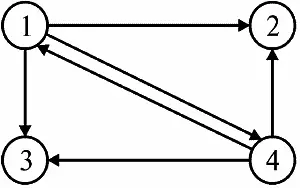
Итак, только что построенный нами граф и является теми данными, для связывания классов сущностей которых и использовалась связь вида сетевой рекурсии.

Из всех видов связей, входящих в рассмотрение нашего конкретного курса лекций, рекурсивными связями являются только две. Мы их уже успели рассмотреть, это соответственно иерархическая и сетевая рекурсивные связи.

Все остальные виды связей, которые нам предстоит рассмотреть, не являются рекурсивными, а представляют собой, как правило, связь нескольких родительских и нескольких дочерних классов сущностей. Причем, как можно догадаться, родительские и дочерние классы сущностей теперь уже никогда не будут совпадать (действительно, ведь речь уже не идет о рекурсии).

Связь, о которой пойдет речь в этом параграфе лекции, называется ассоциацией и относится как раз к нерекурсивному виду связей.

Итак, связь, называемая ассоциацией, реализуется как взаимосвязь между несколькими родительскими классами сущностей и одним дочерним классом сущностей. И при этом, что любопытно, эта взаимосвязь описывается связями различных типов.

Также стоит отметить, что родительский класс сущностей при ассоциации может быть и один, как в сетевой рекурсии, но даже в такой ситуации число связей, идущих от дочернего класса сущностей, должно быть не менее двух.

Интересно, что при ассоциации, так же как и при сетевой рекурсии, существуют специальные виды классов сущностей. Примером такого класса является дочерний класс сущностей. Ведь в общем случае в ассоциации дочерний класс сущностей называется классом ассоциативных сущностей. В частном случае, когда класс ассоциативных сущностей не имеет собственных дополнительных атрибутов и содержит только атрибуты, мигрирующие вместе с первичными ключами из родительских классов сущностей, такой класс называется классом именующих сущностей. Как можно обратить внимание, при этом прослеживается почти абсолютная аналогия с понятием ассоциативных и именующих сущностей в сетевой рекурсивной связи.

Чаще всего ассоциация используется для детализации (разрешения) связей вида «многие ко многим».

Проиллюстрируем это утверждение.

Пусть, например, нам дана следующая презентационная диаграмма, описывающая схему приема некоторого врача в некой больнице:

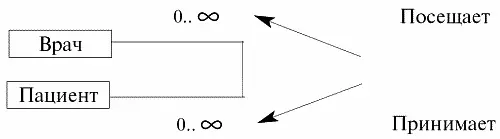
Эта диаграмма буквально означает, что в больнице имеется много врачей и много пациентов, и больше никак отношения и соответствия между врачами и пациентами не отражено. Таким образом, разумеется, что с такой базой данных в администрации больницы никогда не было бы понятно, как проводить приемы у различных врачей различных пациентов. Ясно, что использованные здесь связи типа «многие ко многим» просто необходимо детализировать, чтобы конкретизировать отношения между различными врачами и пациентами, другими словами, чтобы рационально организовать расписание приемов всех имеющихся в больнице врачей и их пациентов.

А теперь построим более подробную ключевую диаграмму, в которой мы уже детализируем все имеющиеся связи «многие ко многим». Для этого мы соответственно введем новый класс сущностей, назовем его «Прием», который будет выступать в роли класса ассоциативных сущностей (позже мы посмотрим, почему именно это будет классом ассоциативных сущностей, а не просто классом именующих сущностей, о которых мы говорили ранее).