Александр Харчевников - Социальный метаболизм. Полилогический матричный анализ «обменных процессов» и стоимости

(0 122 + x 222+0 3 22 )= (0 123 + x 223+0 3 23 ), (37) * 24

(0 131 +0 2 31 + x 331 )= (0 132 +0 2 32 + x 332 ), (38) * 25

(0 131 +0 2 31 + x 331 )= (0 133 +0 2 33 + x 333 ), (39) * 26

(0 132 +0 2 32 + x 332 )= (0 133 +0 2 33 + x 333 ). (40) * 27

В результате получаем, сохраняя (повторяя) при этом прежние номера соответствующих уравнений:

f 11= x 111+ x 112+ x 113= 6000, (4) * 1

f 22= x 221+ x 222+ x 223= 9000, (8) * 5

f 33= x 331+ x 332+ x 333= 12000, (12) * 9

3×x 111= 2×x 221, (16) * 10

2×x 111= 4×x 331, (17) * 11

4× x 221= 3×x 331, (18) * 12

3×x 112= 2×x 222, (21) * 13

2×x 112= 4×x 332, (22) * 14

4×x 222= 3×x 332, (23) * 15

3×x 113= 2×x 223, (26) * 16

2×x 113= 4×x 333, (27) * 17

4×x 223= 3×x 333, (28) * 18

x 111= x 112, (32) * 19

x 111= x 113, (33) * 20

x 112= x 113, (34) * 21

x 221= x 222, (35) * 22

x 221= x 223, (36) * 23

x 222= x 223, (37) * 24

x 331= x 332, (38) * 25

x 331= x 333, (39) * 26

x 332= x 333. (40) * 27

Таким образом сократилось не только число уравнений, но и число неизвестных ограничилось девятью переменными. Эти девять переменных полностью представлены в трёх уравнениях (4) * 1, (8) * 5 и (12) * 9. При этом остальные переменные могут быть выражены через эти девять, что видно по равенствам от (16) * 10 до (40) * 27. В результате и число уравнений, необходимых для получения решения стало равным девяти. Приведём ниже один из вариантов этих «необходимых» уравнений и численную оценку самих переменных.

Рассмотрим равенства (4) * 1, (32) * 19 и (33) * 20:

f 11= x 111+ x 112+ x 113= 6000, (4) * 1

x 111 = x 112, (32) * 19

x 111 = x 113. (33) * 20

Получаем очевидное решение для следующих трёх неизвестных переменных:

x 111= 6000/3 = 2000; x 112= 2000; x 113= 2000.

Далее, рассмотрим равенства (8) * 5, (35) * 22 и (37) * 24:

f 22= x 221+ x 222+ x 223= 9000, (8) * 5

x 221 = x 222, (35) * 22

x 222 = x 223, (37) * 24

Получаем очевидное решение для других трёх неизвестных переменных:

x 222= 9000/3 = 3000; x 221= 3000; x 223= 3000.

Наконец, рассмотрим равенства (12) * 9, (39) * 26 и (40) * 27:

f 33= x 331+ x 332+ x 333= 12000, (12) * 9

x 331 = x 333, (39) * 26

x 332 = x 333. (40) * 27

Получаем очевидное решение для последних трёх неизвестных переменных:

x 333= 12000/3 = 4000; x 331= 4000; x 332= 4000

Таким образом для получения искомого решения оказалось достаточно лишь девяти вышеприведённых уравнений, а именно: (4) * 1, (32) * 19, (33) * 20, (8) * 5, (35) * 22, (37) * 24, (12) * 9, (39) * 26 и (40) * 27. Как ранее было показано прочие переменные этой системы линейных уравнений в данном численном примере равны нулю.

Матрица с численными решениями (численные значения неизвестных переменных в тысячах штук) приведена на рисунке 15. В целях наглядности численные значения неизвестных переменных дополнены (графически) тройными индексами самих переменных, то есть индексами ячеек, элементами которых являются эти переменные.

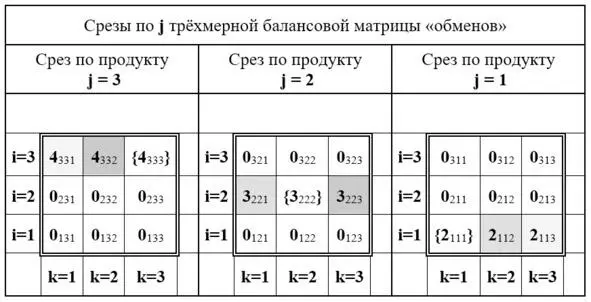
Рис. 15. Балансовая трёхмерная матрица с численными решениями условного примера «обмена» (значения неизвестных переменных даны в тысячах штук)

Из матрицы с численными решениями (см. рис.15, справа внизу – «Срез по продукту j = 1») видно, что агент с индексом i = 1, выступая в роли агента-производителя, отчуждает в пользу агента с индексом k = 3,выступающего в роли агента-потребителя, 2 тысячи (2000) штук продукта с индексом j = 1. Это отображено в ячейке матрицы с координатами: i = 1, j = 1, k = 3, в которой располагается элемент матрицы x ijkс тройным индексом ( 113). Этот тройной индекс последовательно расшифровывается следующим образом: i = 1, j = 1, k = 3.

В то же время (см. рис.15, слева вверху – «Срез по продукту j = 3») агент с индексом i = 3, выступая в роли агента-производителя, отчуждает в пользу агента с индексом k = 1,выступающего в роли агента-потребителя, 4 тысячи (4000) штук продукта с индексом j = 3. Это отображено в ячейке матрицы с координатами: i = 3, j = 3, k = 1, в которой располагается элемент матрицы x ijkс тройным индексом ( 331). Этот тройной индекс последовательно расшифровывается следующим образом: i = 3, j = 3, k = 1.