Алексей Марков - Хулиномика 4.0 [хулиганская экономика. Ещё толще. Ещё длиннее]

Понятно, что если у вас есть тыща долларов, то вторая тыща вас дико обрадует. А если у вас есть миллион, то тыща вас, конечно, обрадует, но не так дико. Тут как в анекдоте про Билла Гейтса: как представить себе его состояние в 50 миллиардов долларов? Очень просто: соберите все свои деньги и добавьте к ним 50 миллиардов долларов.

Теория интересная, но в конце книги мы её немного подрихтуем.

Одна из самых знаменитых разработок в поведенческих финансах – это теория перспектив Канемана и Тверски. Это чуть ли не самая цитируемая работа в экономике. Она о том, как люди делают выбор и почему они делают его нерационально. Старый израильтянин Даниел Канеман до сих пор жив (ему 84), получил нобелевку и написал совершенно гениальную книжку « Thinking, Fast and Slow» (переведена как « Думай медленно, решай быстро »), всем её мощно рекомендую – очищает мысли от шлака.

Но раньше всех об искажениях в оценочной функции человека заговорил американский экономист Пол Самуэльсон, он чуть ли не до ста лет дожил (умер в 2009-м) и до самой смерти подкалывал коллег по полной программе. Однажды за обедом он дико затроллил профессора Кэри Брауна: предложил тому пари на бросок монетки. Самуэльсон предложил выдать коллеге 200 баксов за решку, а за выпавшего орла взять с того лишь $100. В 1963 году, когда состоялось (а точнее, не состоялось) это пари, 100 баксов было значительной суммой денег: как сейчас $774 – я посмотрел по инфляции. Но американские профессора и тогда получали хорошие зарплаты – то есть всё-таки могли позволить себе такую игру.

Вы бы как, сыграли? Если подумать и ответить честно, то вряд ли. Представьте, что кто-то внезапно предлагает вам подкинуть монетку и дать вам 100 тысяч при выигрыше, а при проигрыше вы должны отдать 50. Представили? Хорошо?

Вот и Кэри Браун зассал. Самуэльсон был немного расстроен, хотя и рад тоже. Он сказал: « А если я тебе предложу сыграть 100 раз подряд, ты согласишься? » На сто раз тот был, естественно, согласен, ведь тут никак нельзя оказаться в проигрыше.

Самуэльсон вернулся в офис и написал статью, доказывая, что Кэри Браун нерационален и что он смахивает на кретина. Смысл в том, что нерационально выбирать сто единиц чего-то, если тебе не нужна хотя бы одна единица этого чего-то. Если что-то имеет для тебя ценность (а у сделки положительное матожидание, то есть пари имеет ценность), то рационально принимать любое количество таких пари – и 1, и 10, и 666.

Этот случай послужил мотивационной идеей для Канемана и Тверски. Они начали исследовать вопрос, почему же люди не хотят играть в эту безусловно выгодную для них игру. Простые еврейские ребята предположили, что дело в изломе функции полезности . Знаю, звучит немного абстрактно, но у нас же криптонаучная книга, чего вы хотели. Традиционная функция полезности выглядит как постоянно замедляющаяся растущая кривая [39] Похоже на арктангенс, загуглите. , и теория говорит, что люди принимают решения, исходя из неё. Базовая идея всё ещё в том, что человек хочет больше, потому что полезность он получает как раз от денег.

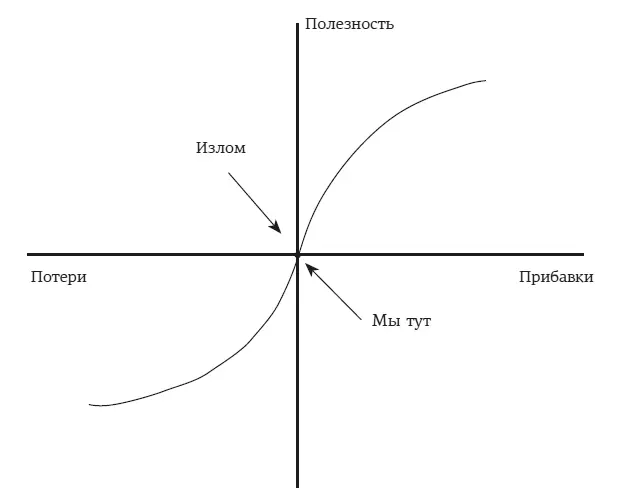
А почему кривая замедляется? Это понятно: каждый дополнительный доллар даёт нам всё меньше счастья, но всё-таки даёт, поэтому нам и хочется больше. Традиционная теория говорит, что пари +$200 / —$100 имеет плюсовое матожидание в $50, и минус $100 не имеет значения на протяжения всей жизни. То есть надо всегда принимать такое пари. Более того, такие сделки надо всё время искать самому, ведь они положительные, а даже минимально положительных ставок нужно делать как можно больше.

На самом деле большинству людей нравится играть в азартные игры иногда, но не постоянно. Они вполне осознанно ходят в казино, где изначально матожидание выигрыша отрицательно. На рулетке это 36/37, то есть в среднем выручка составит примерно девяносто семь центов с каждого поставленного доллара [40], но там всё как-то так красиво обустроено, будто это развлечение.

А вот по жизни люди не ведут себя таким образом, и более того, каждый их конкретный выбор связан с их материальным положением на данный конкретный момент. И у такой – реальной, а не теоретической функции – есть излом. Она не плавная и не постоянная.

В начальной точке – там, где мы сейчас, – функция ломается. Это означает, что для человека потери имеют больший вес, чем аналогичные прибыли. Между выигрышем и проигрышем большая разница – я имею в виду по модулю. Мысль о том, что можно потерять 100 долларов, слишком пугает, и идея принять пари выглядит не такой уж привлекательной. Заработать 200 долларов – это хорошо. По старой теории полезности человек должен был бы сам жадно искать такое пари.