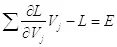 (3.3)
(3.3)
В нерелятивистском случае свободной частицы можно использовать следующие соотношения: 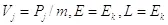 .
.
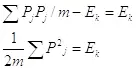 (3.4)
(3.4)
В квантовой механике импульс и энергия являются результатом действия соответствующих операторов на волновую функцию.
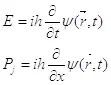 (3.5)
(3.5)
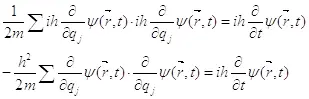 (3.6)
(3.6)
Данное уравнение очень похоже на уравнение Шредингера, и есть всего одно отличие. Под суммой стоят произведения частных производных, в то время как в волновом уравнении используется производная второго порядка. Если использовать в качестве волной функции функцию информации, то данное различие исчезает, так как для информации мы имеем соотношение:
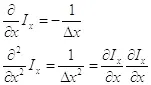 (3.7)
(3.7)
В результате мы получили уравнение для функции информации, которое полностью совпадает с волновым уравнением Шредингера, если использовать нерелятивистские выражения для импульса и энергии.
Для полноты квантово-механической картины рассмотрим соотношения неопределенностей Гейзенберга, лежащие в фундаменте квантовой механики:
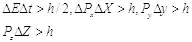 (3.8)
(3.8)
Сравним их с выражениями импульса и энергии объекта:
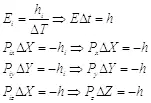 (3.9)
(3.9)
Чтобы получить из данных выражений соотношения неопределенностей, достаточно сказать, что определение координат объекта в пространстве возможно с точностью до половины размера объекта вдоль соответствующей оси при условии отсутствия информации о внутренней структуре объекта.
Получается, что введенное нами понятие физической информации очень хорошо вписывается в квантовую физическую картину и является достаточным для определения большинства физических законов.
В рамках данной работы ставилась задача рассмотрения физических законов с точки зрения такой сущности, как информация. Оказалось, что определение функции информации свободного физического объекта можно получить по правилам математической теории информации через вероятность нахождения объекта в определенной точке пространства. Кроме того, мы получили, что введенная нами функция совпадает с механическим действием, на основе которого построены законы классической механики, а скорость изменения информации является лагранжианом объекта. И самым интересным моментом оказалось то, что функция информации удовлетворяет волновому уравнению Шредингера. Таким образом, можно состыковать классическую и квантовую механику на основе одинаковых понятий. Хотя для этого потребуется убрать несовместимость постулатов, на которых основаны обе эти теории.
Основной предпосылкой квантовой механики является утверждение о том, что частицы не имеют классических траекторий, а существует лишь вероятность нахождения частицы в каждой точке пространства. Такое утверждение полностью противоречит понятиям классической механики, и его необходимо трансформировать к более согласованному виду. В первом разделе мы рассматривали физический объект как две взаимодействующие частицы. И действительно при этом возникают трудности для определения координат такого объекта, связанные с тем, что взаимодействующие частицы находятся в постоянном движении и, не имея точных данных в каждый момент времени о движении частиц, мы можем только обозначить поверхность, за которую данные частицы не выходят или выходят крайне редко. Такая ситуация совпадает с ограничениями квантовой механики и при этом не запрещает объектам иметь непрерывные траектории движения, с которыми работает классическая механика. С точки зрения понятия информации, данное ограничение можно выразить следующим образом. Не имея информации о внутренней структуре объекта, невозможно определить его местоположение в пространстве точнее, чем половина его размера вдоль соответствующей оси.
Данное утверждение не противоречит классической механике и является достаточно простым и понятным для восприятия.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

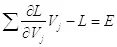 (3.3)
(3.3)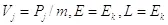 .
.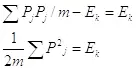 (3.4)
(3.4)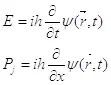 (3.5)
(3.5)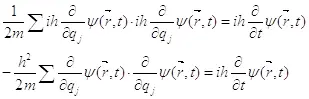 (3.6)
(3.6)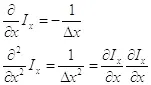 (3.7)
(3.7)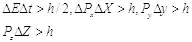 (3.8)
(3.8)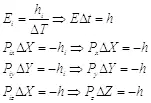 (3.9)
(3.9)






![Анджей Ясинский - Ник - 9 [СИ]](/books/409213/andzhej-yasinskij-nik-9-si-thumb.webp)