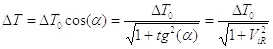 (2.12)
(2.12)
Аналогично пространственный размер объекта будет проекцией 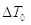 на координатную ось:
на координатную ось:
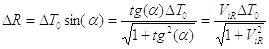 2.13
2.13
Подставив данные выражения в определения энергии и импульса, получим:
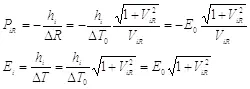 (2.14)
(2.14)
В данных выражениях мы сделали замену двух комплексных коэффициентов на один реальный 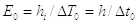 . Данный параметр является энергией объекта при нулевой скорости, и его можно считать энергией покоя объекта. Отсюда можно определить массу покоя, используя выражение энергии из теории относительности:
. Данный параметр является энергией объекта при нулевой скорости, и его можно считать энергией покоя объекта. Отсюда можно определить массу покоя, используя выражение энергии из теории относительности:
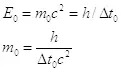 (2.15)
(2.15)
Таким образом, масса покоя определяется как обратный размер объекта с точностью до константы, определяющей единицы измерения. Абсолютно такое же определение будет иметь и энергия покоя.
Теперь вернемся к определению энергии и импульса в теории относительности.
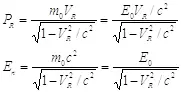 (2.16),
(2.16),
где 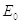 — энергия покоя,
— энергия покоя,
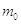 — масса покоя.
— масса покоя.
Если заменить скорость на тангенс угла наклона, получим:
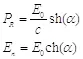 (2.19)
(2.19)
Из данных выражений видно, что релятивистские энергия и импульс являются проекциями энергии покоя (или массы покоя) объекта на соответствующие оси. Таким образом, можно сказать, что у нас есть точное определение физического смысла массы, импульса и энергии покоя.
Подведем итоги данного раздела. Начали мы с того, что нашли выражения для импульса и энергии, используя формулу скорости изменения информации в качестве лагранжиана системы двух взаимодействующих частиц. Оказалось, что в таком случае энергия и импульс являются частными производными от физической информации, которая в свою очередь совпадает с определением действия. Кроме того, выражение для энергии совпало с формулой Планка, определяющей энергию фотона. Одним из главных достижений данного раздела можно считать получение физического смысла такой величины, как масса покоя, на основе которой выражаются понятия энергии и импульса. Полученные нами энергия и импульс являются проекцией обратных размеров объекта на соответствующие оси и не совпадают с выражениями энергии и импульса в релятивистской механике, однако они также являются интегралами движения и на их основе можно рассматривать все физические процессы. Кроме того, при рассмотрении новых величин были замечены элементы квантовой механики, и это позволяет надеяться, что понятие физической информации позволит произвести переход от механики Лагранжа к квантовой механике.
3. Квантовая механика с точки зрения потоков информации
В предыдущем разделе мы получили соотношения между энергией, импульсом и информацией объекта, позволяющие определить законы механического движения:
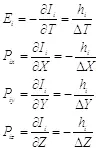 (3.1)
(3.1)
Данные соотношения не совпадают с определениями классической механики, но очень напоминают выражения из квантовой механики. Если произвести переход к реальному времени и подставить значение коэффициента 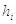 , мы получим комплексные выражения для импульса и энергию, выражаемую формулой Планка:
, мы получим комплексные выражения для импульса и энергию, выражаемую формулой Планка:
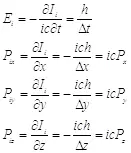 (3.2)
(3.2)
Нетрудно заметить, что импульс является результатом действия оператора импульса 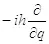 на функцию информации. В квантовой механике, чтобы получить импульс объекта, нужно подействовать оператором импульса на волновую функцию данного объекта. Получается, что функция информации играет роль волновой функции объекта. Это предположение легко проверить при помощи волнового уравнения. Для начала вспомним определение энергии системы через функцию Лагранжа.
на функцию информации. В квантовой механике, чтобы получить импульс объекта, нужно подействовать оператором импульса на волновую функцию данного объекта. Получается, что функция информации играет роль волновой функции объекта. Это предположение легко проверить при помощи волнового уравнения. Для начала вспомним определение энергии системы через функцию Лагранжа.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

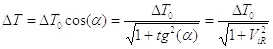 (2.12)
(2.12)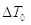 на координатную ось:
на координатную ось: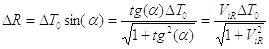 2.13
2.13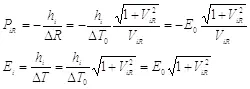 (2.14)
(2.14)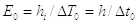 . Данный параметр является энергией объекта при нулевой скорости, и его можно считать энергией покоя объекта. Отсюда можно определить массу покоя, используя выражение энергии из теории относительности:
. Данный параметр является энергией объекта при нулевой скорости, и его можно считать энергией покоя объекта. Отсюда можно определить массу покоя, используя выражение энергии из теории относительности: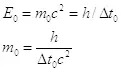 (2.15)
(2.15)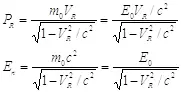 (2.16),
(2.16),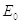 — энергия покоя,
— энергия покоя,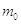 — масса покоя.
— масса покоя.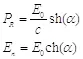 (2.19)
(2.19)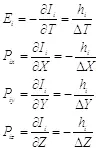 (3.1)
(3.1)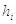 , мы получим комплексные выражения для импульса и энергию, выражаемую формулой Планка:
, мы получим комплексные выражения для импульса и энергию, выражаемую формулой Планка: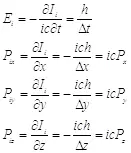 (3.2)
(3.2)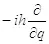 на функцию информации. В квантовой механике, чтобы получить импульс объекта, нужно подействовать оператором импульса на волновую функцию данного объекта. Получается, что функция информации играет роль волновой функции объекта. Это предположение легко проверить при помощи волнового уравнения. Для начала вспомним определение энергии системы через функцию Лагранжа.
на функцию информации. В квантовой механике, чтобы получить импульс объекта, нужно подействовать оператором импульса на волновую функцию данного объекта. Получается, что функция информации играет роль волновой функции объекта. Это предположение легко проверить при помощи волнового уравнения. Для начала вспомним определение энергии системы через функцию Лагранжа.






![Анджей Ясинский - Ник - 9 [СИ]](/books/409213/andzhej-yasinskij-nik-9-si-thumb.webp)