2. Механика с точки зрения потоков информации
Имея функцию Лагранжа для системы, мы можем определить энергию, импульс и законы движения. Так, например, частные производные лагранжиана по компонентам скорости будут являться соответствующими компонентами импульса:
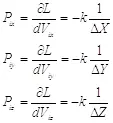 (2.1)
(2.1)
Здесь также нужно отметить, что данные импульсы являются комплексными, так как производные берутся по комплексным скоростям. Если брать производные лагранжиана по обычным скоростям, то добавится множитель ic :
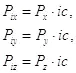
Энергию системы можно получить из лагранжиана, используя следующее выражение:
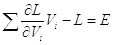 (2.2)
(2.2)
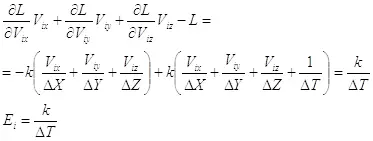 (2.3)
(2.3)
Теперь запишем отдельно выражения для компонент импульса и энергии в реальном времени:
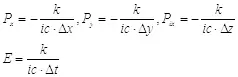 (2.4)
(2.4)
Сразу бросается в глаза, что полученное выражение для энергии совпадает с формулой Планка 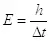 , если определить коэффициент k следующим образом:
, если определить коэффициент k следующим образом:
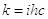 (2.6).
(2.6).
И тогда в реальном пространстве получатся следующие выражения:
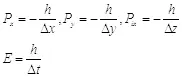 (2.7)
(2.7)
Переменная k играет роль постоянной Планка и определяет единицы измерения энергии и импульса, поэтому обозначим ее буквой 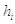 , использовав индекс i по аналогии с другими величинами. Кроме того, переопределим введенную нами функцию физической информации, умножив ее на данную константу, и также добавим к ней индекс i:
, использовав индекс i по аналогии с другими величинами. Кроме того, переопределим введенную нами функцию физической информации, умножив ее на данную константу, и также добавим к ней индекс i:
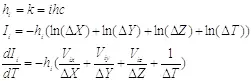 (2.8)
(2.8)
Для удобства приведем в одной таблице все рассмотренные нами величины в случаях пространства Минковского и TR-пространства.
Таблица 1

Данная таблица нам будет очень полезна при переходе рассмотрения между комплексным и метрическим временем.
Глядя на выражения 2.4 и 2.7, можно заметить, что энергия и импульс являются частными производными от информации по координатам и времени:
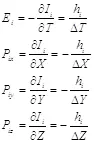 2.9
2.9
Глядя на эти формулы, можно выразить физический смысл энергии и импульса как проекции обратных размеров объекта на соответствующие оси.
Для того чтобы разобраться с импульсами, вернемся к рассмотрению нашего четырехмерного объекта, исключив из него информацию о движении взаимодействующих внутри него частиц. Тогда наш объект будет выглядеть как некоторая четырехмерная поверхность, изображенная на рисунке 2.
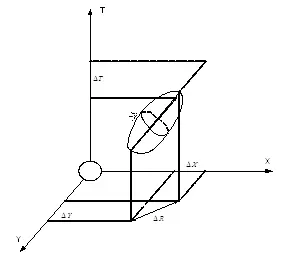
Рисунок 2.
В данной картине можно считать размеры объекта как проекции его четырехмерного размера на различные оси. Тогда они будут определяться по следующим правилам:
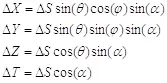 (2.10)
(2.10)
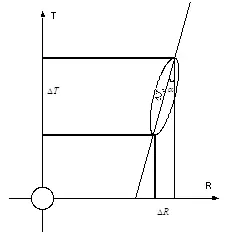
Рисунок 3.
Если выбрать направление одной из координатных осей вдоль движение объекта, то данную картинку можно привести к двумерному виду (Рисунок 3). На данном рисунке показаны четырехмерный объект и зависимость его местоположения от времени R(T). Объект движется с постоянной скоростью, определяемой углом наклона мировой линии к оси времени:
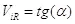 (2.11)
(2.11)
Максимальный размер вдоль временной оси объект будет иметь в собственной системе отсчета, и данный размер обозначен как 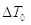 . Во всех остальных системах отсчета размер объекта вдоль временной оси будет являться проекцией объекта на данную ось. Причем размер
. Во всех остальных системах отсчета размер объекта вдоль временной оси будет являться проекцией объекта на данную ось. Причем размер 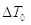 является инвариантом в любых системах отсчета и его можно считать неизменной характеристикой объекта при условии, что форма объекта не меняется:
является инвариантом в любых системах отсчета и его можно считать неизменной характеристикой объекта при условии, что форма объекта не меняется:
Читать дальше
Конец ознакомительного отрывка
Купить книгу

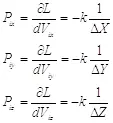 (2.1)
(2.1)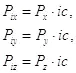
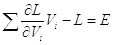 (2.2)
(2.2)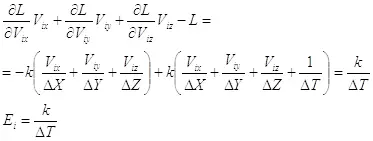 (2.3)
(2.3)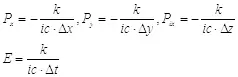 (2.4)
(2.4)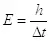 , если определить коэффициент k следующим образом:
, если определить коэффициент k следующим образом: (2.6).
(2.6).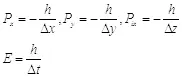 (2.7)
(2.7)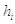 , использовав индекс i по аналогии с другими величинами. Кроме того, переопределим введенную нами функцию физической информации, умножив ее на данную константу, и также добавим к ней индекс i:
, использовав индекс i по аналогии с другими величинами. Кроме того, переопределим введенную нами функцию физической информации, умножив ее на данную константу, и также добавим к ней индекс i: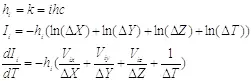 (2.8)
(2.8)
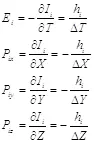 2.9
2.9
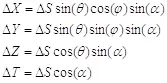 (2.10)
(2.10)
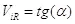 (2.11)
(2.11)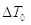 . Во всех остальных системах отсчета размер объекта вдоль временной оси будет являться проекцией объекта на данную ось. Причем размер
. Во всех остальных системах отсчета размер объекта вдоль временной оси будет являться проекцией объекта на данную ось. Причем размер 






![Анджей Ясинский - Ник - 9 [СИ]](/books/409213/andzhej-yasinskij-nik-9-si-thumb.webp)