Грег Иган - Лестница Шильда

Но в действительности такого коллапса не происходит. Если измерения произвести с объединенной системой, А + В , окажется, что она находится в чистом квантовом состоянии, а все компоненты исходного вектора состояния системы А сохранились. Классической физикой потому и пользуются, что полная информация, необходимая для обнаружения квантовых феноменов на макроуровне, нам, как правило, недоступна.

На моем сайте:

http: //gregegan.customer.netspace.net .а u / SCHILD / Decoherence / DecoherenceApplet . html

доступен с тремя экспериментами, в которых показано, как извлечь, казалось бы, потерянную информацию о состоянии запутанной части составной системы при наблюдении за системой в целом.

Спиновые сети ― состояния квантовой геометрии в теории квантовой гравитации, открытые Ли Смолиным и Карло Ровелли. Это понятие — ключевой концептуальный предшественник вымышленной физики «Лестницы Шильда».

Одним из способов описания геометрии пространства выступает описание способа, каким векторы переносятся вдоль любого пути — этот процесс известен под названием «параллельного переноса». В искривленном пространстве параллельный перенос по петле обычно поворачивает вектор относительно исходного направления; известным следствием отсюда выступает тот факт, что при этом сумма углов треугольника отличается от 180 градусов.

Если квантовомеханическая частица переносится по определенному пути в пространстве, начиная его со спином j ,компонента которого вдоль оси Z равна т, параллельный перенос, вообще говоря, изменит значение спинового состояния частицы. Это явление в квантовой механике соответствует повороту классического вектора. Например, если электрон начинает перемещение со спином ↑, он может перейти в состояние суперпозиции компонент со спинами ↑и ↓или же изменить фазу; это зависит от того, какое именно вращение он претерпевает, то есть от кривизны области пространства, которую электрон пересекает. Итак, простым способом определения геометрии пространства видится следующий: взять электрон, перенести его по петле и посмотреть, как изменилось спиновое состояние частицы.

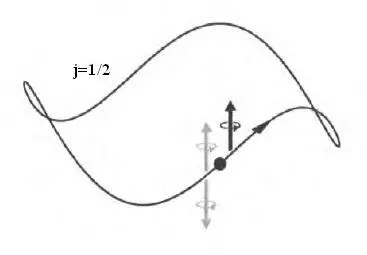
Спиновые сети представляют собой обобщение этой идеи, но сравнение производится более сложным образом. Каждому ребру спиновой сети приписывают значение спина j . Можно представить себе параллельный перенос частиц вдоль каждого ребра, так что их суммарный спин соответствует j . В каждом узле вычисляется амплитуда, которой выражено различие спиновых состояний на входе и выходе. Произведение амплитуд всех узлов дает общий спин сети, зависящий от геометрии пространства, куда погружены ребра сети.

Общие значения спина на ребрах недостаточно полно описывают спиновое состояние частиц: сохраняется произвол при выборе значений m , компоненты спина вдоль оси Z . Трудность в том, что, если задаться определенным значением этой компоненты (скажем, принять m = j для всех ребер), то для каждого типа геометрии амплитуды будут зависеть от ориентации оси Z . Тем не менее существует простой способ превозмочь эту проблему: если просуммировать амплитуду сети по всем возможным комбинациям значений m , где т пробегает диапазон значений — j…+ j на каждом ребре, получим величину, полностью независимую от выбора ориентации.

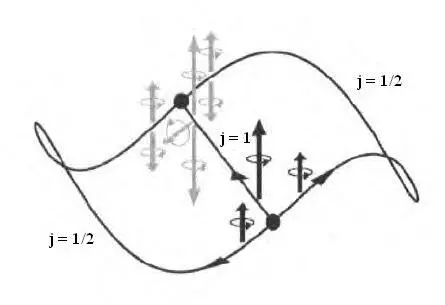
С использованием этой суммы спиновая сеть позволяет определить состояние квантовой геометрии, характеризующееся ценным свойством, а именно калибровочной инвариантностью: амплитуда не зависит от способа измерения, но только от геометрии пространства внутри сети.

На моем сайте доступен:

http: //gregegan.customer.netspace.net.au/SCHILD/Spin/Spin.html ,

где для разных геометрийпостроены различные состояния спиновых сетей.

Эффект параллельного переноса вектора по определенному маршруту можно представить в виде карты линий, соединяющих касательные пространства в начальной и конечной точках маршрута. Говорят, что для этого пути наблюдается голономия , выраженная вращением R .Семейство геометрий, для которых вышеуказанный апплет вычисляет эволюцию спиновой сети, характеризуется простым правилом: параллельный перенос по прямой из точки (х 0, у 0, z 0)в точку (x 1,y 1,z 1 )поворачивает вектор вокруг оси а на угол, равный магнитуде a , причем