ТАБЛИЦА ПРОСТЕЙШИХ ПИФАГОРОВЫХ ТРОЕК
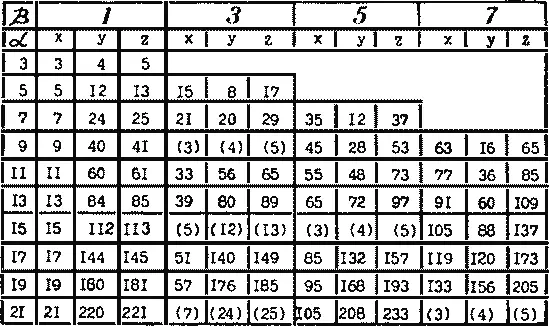
(Цифры в скобках получаются после сокращения на общий множитель и равны цифрам столбца при β = 1.)
— Не могу отказать вам в математическом остроумии, но нахождение вывода старых формул не может подняться до значения самих этих формул. Так что я не вижу, к сожалению, смысла в вашей умственной расточительности ради повторения давно человечеством пройденного.
Пьер Ферма покраснел, потом побледнел, пронизывающе смотря на составленную им таблицу рядов, которую в эту минуту изучал арабский звездочет.
— Простите мне во имя аллаха, мои высокочтимые гости, что я рискую обратить ваше внимание на то, что в составленной молодым гостем таблице я вижу весьма примечательные особенности, которые, надо думать, он подметил и обосновал. Кроме того, можно увидеть, что тройки, вычисленные по древним формулам, не окажутся, как в таблице господина Пьера Ферма, простейшими числами. Произвольно задаваясь величинам m и n, мы получим после вычислений хаотические, беспорядочные, как россыпь разноцветных камней, значения всевозможных прямоугольных треугольников, отнюдь не способствующих выявлению законов их построения.
— Вы правы, уважаемый Мохаммед эль Кашти, таблица троек действительно дает возможность установить некоторые зависимости как в вертикальных рядах, так и в рядах, соседствующих по горизонтали. — И он познакомил слушателей с тем, что открыл [17] Примечание автора для особо интересующихся. Вертикальные ряды x представляют собой арифметические прогрессии с показателем = 2 β . Все значения сторон треугольников с возрастанием ряда изменяются по арифметической прогрессии, показатель которой для y — постоянен и равен 4, а для x и z увеличивается с порядковым номером ряда и порядкового номера тройки в вертикальном ряду и равен 4 ( β + i — 1), где i — порядковый номер тройки в ряду.
. По просьбе арабского ученого особенно остановился Пьер Ферма на выборе коэффициента α и β в своих формулах.
— Вас интересует, уважаемый Мохаммед эль Кашти, случай, когда коэффициенты a и b содержат общий множитель √21? — И он показал с убедительной простотой, что в этом случае получающиеся тройки будут повторять все первые тройки соседних по горизонтали рядов [18] Примечание автора для особо интересующихся. Если α = p√2e, β = q√2e , то p и q могут быть и четными и нечетными, x = αβ = 2 pqe, y = ( p 2 — q 2 ) e; z = ( p 2 + q 2 ) e , то есть p и q тождественны m и n древних формул (см. пред. примеч.), x и y просто меняются местами, к тому же, помноженные на e , не являются простейшими.
.
— Вы убедили меня, почтенный знаток и поэт чисел. Видит аллах, с каким благоговением я стараюсь вникнуть в найденные вами числа и мудро расставленные по клеткам таблицы, кажущейся мне поистине волшебной. Но я покажу почтенным господам, какие тайны хранит в себе эта простенькая таблица.
— Что же вы обнаружили в ней, уважаемый Мохаммед эль Кашти? Разве я не все понял в собственной работе?
— Конечно, не все, ибо все понятно лишь одному всемогущему аллаху! Но достаточно прикоснуться к математическому сокровищу, чтобы обнаружить в нем…
— Что же? Что? — нетерпеливо торопил арабского звездочета Пьер Ферма.
— Благословенное аллахом золотое сечение! 8 единиц рассекаются на 5 и 3, 13 — на 8 и 5! А эти цифры стоят в таблице поблизости, как и в орнаменте [19] Примечание автора для особо интересующихся. Золотое сечение было известно древним зодчим, но сформулировано Леонардо да Винчи. Цифры 3, 5, 8, 13 совпадают с частью ряда Фибаначчи, помогающего современным ученым объяснять ряд явлений природы (1, 1, 2, [3, 5, 8, 13,] 21, 34 и т. д.).
!
Декарт скептически пожал плечами и поморщился. Араб воскликнул:
— Видит аллах справедливый, что вы напрасно так холодны, господин Картезиус! В этой премудрой таблице египетских рядов, как в бездонном колодце, можно черпать сокровища знаний.
— Я не хочу отказывать древним в важных познаниях, но я не вижу причин искать закономерности построения треугольников, будучи не уверен в их практической ценности, поскольку величины сторон ограничены такой условностью, как целочисленность.
— О многочтимый господин Картезиус! Я с почтительным вниманием изучаю ваши латинские труды по философии, стараясь вникнуть в глубину ваших мыслей, но позвольте возразить вам, не оспаривая вашего права на высказанное мнение.
Читать дальше












