Александр Казанцев - Собрание сочинений в трех томах. Том 2. Клокочущая пустота.

Омнибус, предложенный Б. Паскалем. (Примеч. авт.)

Примечание автора для особо интересующихся. Метод Ферма, в свое время несправедливо оспоренный Декартом, предвосхищал дифференциальное и интегральное исчисление, хотя задачу решал алгебраически, без анализа бесконечно малых величин. В задаче разбивки прямой с длиной « a » на две части, так, чтобы квадрат одной ( x 2), помноженный на величину другой части = ( a — x ), был бы максимальным, он приравнивал 2 ax — 3 x 2к нулю и получал, что x = 2/ 3 a , то есть заменял современное дифференцирование и взятие первой производной.

Правота Торричелли была подтверждена знаменитым опытом Герике, получившим название «Магдебургские полушария», проведенным в Магдебурге лишь в 1654 году и доказавшим существование атмосферного давления. Торричелли принадлежит изобретение ртутного барометра и создание над ртутным столбом «торричеллиевой пустоты». (Примеч. авт.)

Примечание автора для особо интересующихся . Автору удалось восстановить позицию

См. левую диаграмму. Последовало: 1. Л: g1! ( 1. e7? fg 2. e8Ф Кf8+ 3. Крd8 Л: e8+ 4. Кр: e8 с шансами у черных) Л: g1 2. Сe5+! de 3. e7 Л: g5 4. Кd5 Кf6 5. К: f6 Кр: f6 6. e8К мат!

См. правую диаграмму. 6. e8Ф? f4 7. Фe7 + Крf5 8. Ф: f7 + Крg4 9. Фe6 + Лf5! 10. Ф: g6 + Л: g5 11. Фe6 + Лf5 12. Фg8 + Лg5, в лучшем случае для белых — ничья.

Эта мысль была высказана британским генералом на три с четвертью столетия раньше, чем в наше время (когда она звучит уже угрозой самому существованию человечества) американским генералом Александром Хейгом в бытность его государственным секретарем в администрации президента Р. Рейгана. (Примеч. авт.)

В своем знаменитом «втором вызове» английским математикам в феврале 1657 года Пьер Ферма, предложив им решить указанное уравнение с названными коэффициентами, писал: «Я жду решения этих вопросов: если оно не будет дано ни Англией, ни Бельгийской или Кельтской Галлией, то это будет сделано Нарбоннской Галлией…». Уравнение это, получив название уравнения Пелля (без достаточных исторических оснований), теперь охотнее именуется уравнением Ферма, исследованное впоследствии Эйлером и окончательно проанализированное Лагранжем. (Примеч. авт.)

Швейцарская легенда повествует о необычайно метком стрелке, народном герое Вильгельме Телле, которого враги принудили сбить стрелой яблоко с головы любимого сына. (Примеч. авт.)

Переписка ученых, собранная Джоном Валлисом, вошла приложением к третьему тому сочинений Пьера Ферма на французском языке в 1679 году, выпущенных его сыном Самуэлем. (Примеч. авт.)

Это письмо к Каркави получило название «Завещание Ферма». (Примеч. авт.)

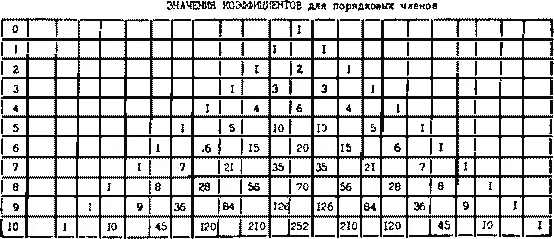
Примечание автора для особо интересующихся. Рассмотренный Паскалем «бином», впоследствии названный «биномом Ньютона», известен ныне как: ( x + y ) 0= 1; ( x + y ) 1= z ; ( x + y ) 2= x 2+ 2 xy + y 2; ( x + y ) 3= x 3+ 3 x 2 у + 3 xy 2+ y 3; ( x + y ) 4= x 4+ 4 x 3 y 2+ 6 x 2 y 2+ 4 xy 3+ y 4и т. д.

В своем 42-м замечании на полях книги «Арифметика» Диофанта Пьер Ферма записал по-латыни: «…наука о целых числах, которая, без сомнения, является прекраснейшей и наиболее изящной, не была до сих пор известна ни Боше, ни кому-либо другому, чьи труды дошли до меня (Боше де Мазариак — математик, издавший в переводе на латынь с древнегреческого «Арифметику» Диофанта, снабдив ее своими комментариями и дополнениями, ставшую настольной книгой Ферма). (Примеч. авт.)

Примечание автора для особо интересующихся.

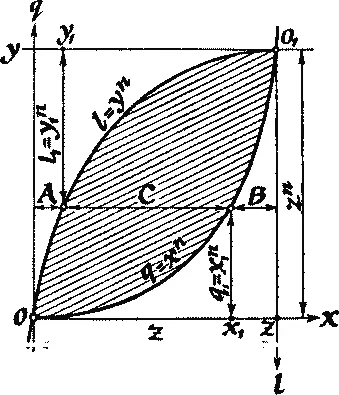
Метод совмещенных парабол Пьера Ферма сводится к тому, что в системе прямоугольных координат (декартовых!) с горизонтальной осью x и вертикальной q — ( xO 1q ) — вычерчивается парабола по уравнению q = x n . Чертеж поворачивается на 180°, и на нем наносится (см. рис.) еще одна система прямоугольных координат ( yO 1l ) с горизонтальной осью « у » и вертикальной « l ». Вертикальные оси двух систем координат отстоят одна от другой на величину z , а горизонтальные на z n . В перевернутой системе координат тоже вычерчивается точно такая же парабола по уравнению l = y n . Две совмещенные таким способом параболы образуют полусимметричную геометрическую фигуру, ограниченную ими. Выбирая точку x 1 на оси x , строим от нее вертикальный отрезок (до пересечения с первой построенной параболой) с длиной g 1= x 1 n . Проведя теперь горизонтальную линию от пересечения вертикального отрезка с параболой через фигуру до второй параболы, получим точку, вертикальный отрезок от которой до оси у перевернутой координатной системы отметим на оси y точку y 1. Длина же этого отрезка, равная ординате перевернутой параболы, будет l = y n . Из построения следует: q + l 1= x 1 n + y 1 n = z 1 n . Диофантово уравнение, положенное Ферма в основу его Великой теоремы. Все это восстановлено А. Н. Кожевниковым.