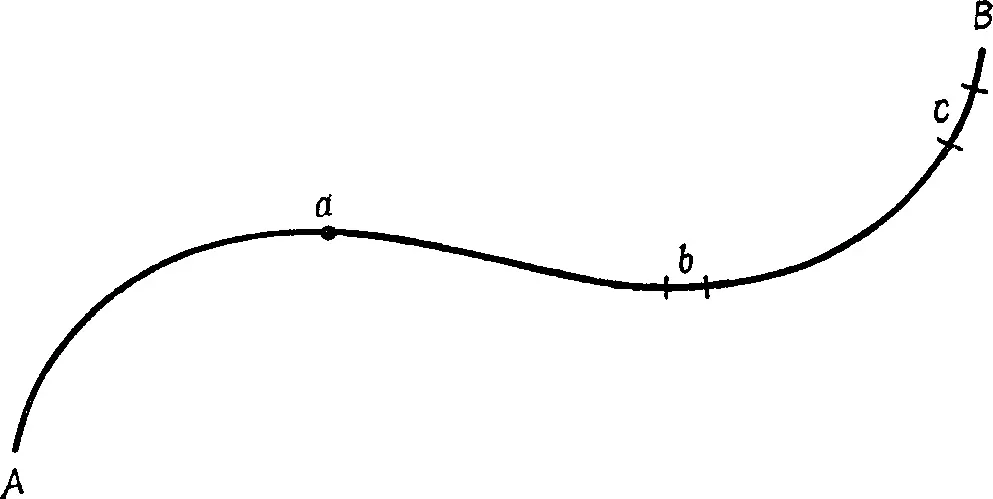
Рис. 1.
Мы начнем с того, что рассмотрим, как ограничено восприятие пространства у существа, живущего в мире одного измерения, то есть на бесконечной кривой в пространстве, конечный отрезок AB которой мы условно изобразим на рис. 1. Предположим, что в различных точках этой кривой находятся три существа a, b и с, причем существо а имеет вид точки, существо b — небольшого отрезка, а существо с по форме напоминает существо b, но имеет несколько большую длину. Мы различаем существа а, b и с по форме потому, что наблюдаем за ними извне. Однако существу а другое существо b представляется в виде точки, так же как существу b — существо с. Такое «точечное» восприятие обусловлено тем, что одномерным существам известно лишь расстояние (вдоль кривой) и положение на ней. Все остальное, что так или иначе связано с каким-нибудь третьим геометрическим свойством, для одномерных обитателей кривой лишено смысла. Существо а, наблюдая существо b , может видеть его лишь в виде точки, потому что смотрит «в торец» отрезку b. Предположим, что существа а, b и с сохраняют свое относительное расположение на кривой на протяжении всей своей жизни. Поскольку каждое из существ в этом случае будет располагать лишь весьма ограниченными сведениями о жизни двух других обитателей кривой, то они будут строить различные умозаключения о том, что представляют собой их соседи. Так, существо а, сознавая собственную точечную форму и видя существо b лишь с «торца», сделает вполне логичный, хотя и неправильный вывод: на кривой обитают лишь точечные существа. Существо b, сознавая свою длину и видя своих соседей а и с в виде точек, решит, что оно удостоилось особой милости творца, вознесшего его в нарушение всех законов природы над его собратьями по пространству.
На рис. 1 мы изобразили произвольную кривую, или траекторию, в пространстве, но для того, чтобы избежать излишних усложнений на последующих рисунках, мы в дальнейшем условимся изображать одномерное пространство в виде прямой. Отрезок прямой можно рассматривать как траекторию точки, ограниченную ее начальным и конечным положением в пространстве. Отрезок прямой — это частный случай движения точки из одного положения в другое по кратчайшему пути AB (рис. 2). Если отрезок AB мы передвинем по кратчайшему пути из начального в конечное положение A'В', то получим плоскую фигуру — прямоугольник. Если отрезок AB переместится по кратчайшему пути па расстояние, равное своей длине (рис. 3), то получится плоская фигура, которая называется «квадрат». Таким образом, квадрат можно назвать элементарной фигурой в двумерном мире, так же как отрезок прямой мы называем элементарной фигурой в одномерном мире.
Переходя от линейного мира к плоскому, мы обнаруживаем, что число различных форм геометрических фигур неизмеримо возросло. Так, в нашем двумерном мире могут существовать не только обитатели, имеющие вид точек и прямолинейных отрезков, но и многочисленные раньше. Точка P будет свободно перемещаться по всей плоскости, явно «не желая» расставаться е двумерным миром, хотя в действительности она принадлежит прямой, способной разместиться лишь в трехмерном пространстве.
Перейдем теперь к рассмотрению знакомых всем нам предметов, а именно предметов, находящихся в трехмерном пространстве. Все формы материи, доступные нашим ощущениям, занимают некоторую часть пространства и обладают длиной, шириной и высотой. Плоскость, прямая и точка существуют в теории лишь для того; чтобы человек мог строить приближенные образы в соответствии с тем, что он наблюдает в материальном мире. Природа действует посредством универсальных законов и строит применительно к условиям, руководствуясь неписаными законами экономии. Прямая и плоскость встречаются в природе исключительно редко, главным образом среди низших форм растений и животных, но человек, пренебрегая более тонкими соображениями, определяющими выбор тех или иных средств в природе, и постоянно совершая ошибки, вынужден достигать своих целей простейшими и наиболее прямыми из доступных ему методов. Поэтому он принимает за единицу длины некий отрезок прямой, за единицу площади — плоскую фигуру, известную под названием квадрата, и за единицу объема — тело, ограниченное шестью гранями и известное под названием куба. Мы видели, что на плоскости квадрат можно построить, перемещая отрезок в перпендикулярном ему направлении на расстояние, равное длине отрезка. Аналогично можно построить и куб в трехмерном пространстве. Представим себе, что квадрат ABА'В' (рис. 3) перемещается па расстояние, равное длине любой из его сторон, в направлении, перпендикулярном плоскости квадрата. В результате такого перемещения мы получим (рис. 7) трехмерную фигуру — куб.
Читать дальше













