Arthur Clarke - The Ghost from the Grand Banks

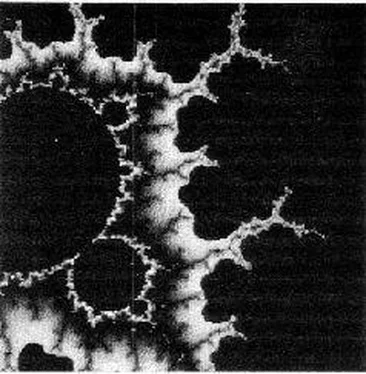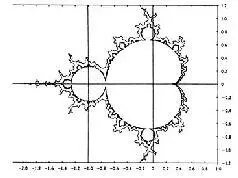
The boundary—if one can call it that—of the M-Set is not a simple line; it is something which Euclid never imagined, and for which there is no word in ordinary language. Mandelbrot, whose command of English (and American) is awesome, has ransacked the dictionary for suggestive nouns. A few examples: foams, sponges, dusts, webs, nets, curds. He himself coined the technical name fractal , and is now putting up a spirited rearguard action to stop anyone from defining it too precisely.

Computers can easily make “snapshots” of the M-Set at any magnification, and even in black and white they are fascinating. However, by a simple trick they can be colored, and transformed into objects of amazing, even surreal, beauty.

The original equation, of course, is no more concerned with color than is Euclid’s Elements of Geometry . But if we instruct the computer to color any given region in accordance with the number of times z goes around the loop before it decides whether or not it belongs to the M-Set, the results are gorgeous.

Thus the colors, though arbitrary, are not meaningless. An exact analogy is found in cartography. Think of the contour lines on a relief map, which show elevations above sea level. The spaces between them are often colored so that the eye can more easily grasp the information conveyed. Ditto with bathymetric charts; the deeper the ocean, the darker the blue. The mapmaker can make the colors anything he likes, and is guided by aesthetics as much as geography.

It’s just the same here—except that these contour lines are set automatically by the speed of the calculation—I won’t go into details. I have not discovered what genius first had this idea—perhaps Monsieur M. himself—but it turns them into fantastic works of art. And you should see them when they’re animated…

One of the many strange thoughts that the M-Set generates is this. In principle, it could have been discovered as soon as the human race learned to count. In practice, since even a “low magnification” image may involve billions of calculations, there was no way in which it could even be glimpsed before computers were invented! And such movies as Art Matrix’ Nothing But Zooms would have required the entire present world population to calculate night and day for years—without making a single mistake in multiplying together trillions of hundred-digit numbers…

I began by saying that the Mandelbrot Set is the most extraordinary discovery in the history of mathematics. For who could have possibly imagined that so absurdly simple an equation could have generated such—literally—infinite complexity, and such unearthly beauty?

The Mandelbrot Set is, as I have tried to explain, essentially a map. We’ve all read those stories about maps which reveal the location of hidden treasure.

Well, in this case—the map is the treasure!

Colombo, Sri Lanka

1990 February 28