Arthur Clarke - The Ghost from the Grand Banks

.99999999999999999999

As before, nothing much happens for a long time as we go around the loop, except that the numbers on the far right get steadily smaller. But after a few thousand or million iterations—catastrophe! Z suddenly shrinks to nothing, dissolving in an endless string of zeros…

Check it out on your computer. It can only handle twelve digits? Well, no matter how many you had to play with, you’d still get the same answer. Trust me…

The results of this “program” can be summarized in three laws that may seem too trivial to be worth formulating. But no mathematical truth is trivial, and in a few more steps these laws will take us into a universe of mind-boggling wonder and beauty.

Here are the three laws of the “Squaring” Program:

1. If the input z is exactly equal to 1, the output Z always remains 1.

2. If the input is more than 1, the output eventually becomes infinite.

3. If the input is less than 1, the output eventually becomes zero.

That circle of radius 1 is therefore a kind of map—or, if you like, fence—dividing the plane into two distinct territories. Outside it, numbers which obey the squaring law have the freedom of infinity; numbers inside it are prisoners, trapped and doomed to ultimate extinction.

At this point, someone may say: “You’ve only talked about ranges —distances from the origin. To fix the blip’s position, you have to give its bearing as well. What about that?”

Very true. Fortunately, in this selection process—this division of the z ’s into two distinct classes—bearings are irrelevant; the same thing happens whichever direction r is pointing. For this simple example—let’s call it the S-set—we can ignore them. When we come on to the more complicated case of the M-Set, where the bearing is important, there’s a very neat mathematical trick which takes care of it, by using complex or imaginary numbers (which really aren’t at all complex, still less imaginary). But we don’t need them here, and I promise not to mention them again.

The S-set lies inside a map , and its frontier is the circle enclosing it. That circle is simply a continuous line with no thickness. If you could examine it with a microscope of infinite power, it would always look exactly the same. You could expand the S-set to the size of the Universe; its boundary would still be a line of zero thickness. Yet there are no holes in it; it’s an absolutely impenetrable barrier, forever separating the z ’s less than one from those greater than one.

Now, at last, we’re ready to tackle the M-Set, where these commonsense ideas are turned upside down. Fasten your seat belts.

During the 1970s, the French mathematician Benoit Mandelbrot, working at Harvard and IBM, started to investigate the equation which has made him famous, and which I will now write in the dynamic form:

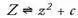
The only difference between this and the equation we have used to describe the S-set is the term c . This—not z —is now the starting point of our mapping operation. The first time around the loop, z is put equal to zero.

It seems a trifling change, and no one could have imagined the universe it would reveal. Mandelbrot himself did not obtain the first crude glimpses until the spring of 1980, when vague patterns started to emerge on computer printouts. He had begun to peer through Keats’

As we shall learn later, that word “foam” is surprisingly appropriate.

The new equation asks and answers the same question as the earlier one: What shape is the “territory” mapped out when we put numbers into it? For the S-set it was a circle with radius 1. Let’s see what happens when we start with this value in the M-equation. You should be able to do it in your head—for the first few steps. After a few dozen, even a supercomputer may blow a gasket.

For starters, z = 0, c = 1. So Z = 1

First loop: Z = 1 2+ 1 = 2

Second loop: Z = 2 2+ 1 = 5

Third loop: Z = 5 2+ 1 = 26

Fourth loop: Z = 26 2+ 1… and so on.

I once set my computer to work out the higher terms (about the limit of my programming ability) and it produced only two more values before it had to start approximating:

1, 2, 5, 26, 677, 458330,

21006640000

4412789000000000000000

At that point it gave up, because it doesn’t believe there are any numbers with more than 38 digits.

However, even the first two or three terms are quite enough to show that the M-Set must have a very different shape from the perfectly circular S-set. A point at distance 1 is in the S-set; indeed, it defines its boundary. A point at that same distance may be outside the boundary of the M-Set.

Note that I say “may,” not “must.” It all depends on the initial direction, or bearing, of the starting point, which we have been able to ignore hitherto because it did not affect our discussion of the (perfectly symmetrical) S-set. As it turns out, the M-Set is only symmetrical about the X, or horizontal, axis.

One might have guessed that, from the nature of the equation. But no one could possibly have intuited its real appearance. If the question had been put to me in virginal pre-Mandelbrot days, I would probably have hazarded: “Something like an ellipse, squashed along the Y-axis.” I might even (though I doubt it) have correctly guessed that it would be shifted toward the left, or minus, direction.

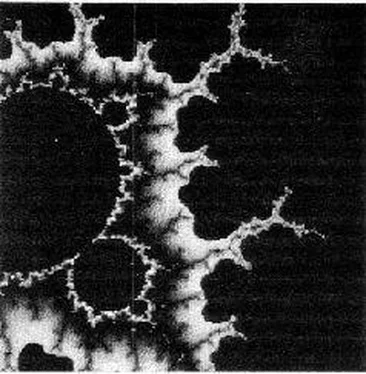
At this point, I would like to try a thought experiment on you. The M-Set being literally indescribable, here’s my attempt to describe it:

Imagine you’re looking straight down on a rather plump turtle, swimming westward. It’s been crossed with a swordfish, so has a narrow spike pointing ahead of it. Its entire perimeter is festooned with bizarre marine growths—and with baby turtles of assorted sizes, which have smaller weeds growing on them…

I defy you to find a description like that in any math textbook. And if you think you can do better when you’ve seen the real beast, you’re welcome to try. (I suspect that the insect world might provide better analogies; there may even be a Mandelbeetle lurking in the Brazilian rain forests. Too bad we’ll never know.)

Here is the first crude approximation, shorn of details—much like Conroy Castle’s “Lake Mandelbrot” (Chapter 18). If you like to fill its blank spaces with the medieval cartographers” favorite “Here be dragons” you will hardly be exaggerating.

First of all, note that—as I’ve already remarked—it’s shifted to the left (or west, if you prefer of the S-set, which of course extends from +1 to -1 along the X-axis. The M-Set only gets to 0.25 on the right along the axis, though above and below the axis it bulges out to just beyond 0.4.

On the left-hand side, the map stretches to about -1.4, and then it sprouts a peculiar spike—or antenna—which reaches out to exactly -2.0. As far as the M-Set is concerned, there is nothing beyond this point; it is the edge of the Universe. Mandelbrot fans call it the “Utter West,” and you might like to see what happens when you make c equal to -2. Z doesn’t converge to zero—but it doesn’t escape to infinity either, so the point belongs to the set— just . But if you make c the slightest bit larger, say -2.00000… 000001, before you know it you’re passing Pluto and heading for Quasar West.

Now we come to the most important distinction between the two sets. The S-set has a nice, clean line for its boundary. The frontier of the M-Set is, to say the least, fuzzy. Just how fuzzy you will begin to understand when we start to “zoom” into it; only then will we see the incredible flora and fauna which flourish in that disputed territory.