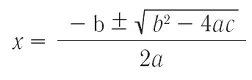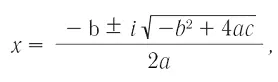Макс Кидрук - Бот

Хтозна, може, я помиляюсь, і пісня майне повз вас, не зачепивши життєво важливих органів… Ну що ж, тоді просто позліть сусідів громоподібним ревінням динаміків:)

М. К.

14 січня 2012

хостел «Cardboard Box Backpackers»

Віндхук, Намібія

P. S. Епізод, у якому Ріно Хедхантер розстрілює ботів зі снайперської гвинтівки, підловивши «малюків» у найінтимніший момент їхнього короткого і такого нелегкого життя, присвячується Квентіну Тарантіно та Чаку Паланіку.

П еред тим як перейти до розгляду множини (фрактала) Мандельброта, пригадаємо, що таке звичайне квадратне рівняння (ми всі вивчали їх у початкових класах школи), а також те, як вони розв’язуються. Саме через такі рівняння найлегше збагнути поняття комплексних чисел та комплексної площини.

Квадратним рівняння називається алгебраїчне рівняння виду:

ax 2+ bx + c = 0,

де a, b і c — коефіцієнти, x — змінна.

Це рівняння має дварозв’язки (корені), що визначаються з виразу:

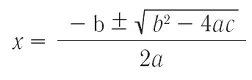
В загальному вираз b 2— 4 ac , з якого добувається корінь квадратний у чисельнику, може бути будь-яким — як додатним, так і від’ємним. У випадку b 2— 4 ac ≥ 0 проблем не виникає — рівняння розв’язується і має два корені. Що ж виходить, коли b 2— 4 ac < 0, і під коренем квадратним опиняється від’ємне число? До п’ятого чи шостого класу нас учили, що таке рівняння не розв’язується. Коренів просто не існує. Це твердження обґрунтовувалось неможливістю видобування кореня квадратного з від’ємного числа. Насправді все зовсім не так просто.

В математиці немало задач, під час розв’язку яких доводиться добувати корені з від’ємних чисел. Для того, щоб подолати цю проблему, математики вигадали цікаву штуку, яку назвали уявна одиниця і позначили і . Уявна одиниця — це таке число, квадрат якого дорівнює мінус одиниці. Тобто, i 2= -1. Таким чином, розв’язати квадратне рівняння можна навіть при b 2— 4 ac < 0. Корені в такому випадку матимуть вигляд:

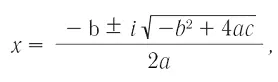
де і — уявна одиниця.

А тепер забудьте про квадратні рівняння і сконцентруйтесь на ідеї уявної одиниці. Введення поняття числа і призвело до появи комплексних чисел.

В загальному, комплексні числа — це розширення дійсних чисел, якими ми зазвичай користуємося при лічбі. Будь-яке комплексне число z записується у вигляді:

z= x + iy ,

де x та y — звичайні (дійсні) числа, і — уявна одиниця.

Тривалий час комплексні числа сприймались як абстракція, вигадана математиками і придатна лиш для математичних головоломок. Нині комплексні числа дозволяють зручно і стисло сформулювати чимало математичних моделей, їх застосовують у математичній фізиці та природничих науках (електротехніці, гідродинаміці, квантовій механіці, теорії коливань тощо). Власне, якби не комплексні числа, вчені б досі не мали уявлення про фрактальну геометрію, а також про надскладну впорядкованість природи.

Комплексні числа можна представити геометрично (візуально). Візьмемо площину з прямокутною (Декартовою) системою координат. На осі абсцис відкладатимемо значення x, на осі ординат — y (див. рис. нижче). Будь-яке комплексне число (z 0= x 0+ iy 0 чи z 1= x 1 + iy 1) можна представити у вигляді точки на цій площині (відповідно, з координатами {x 0, y 0} та {x 1, y 1}). Ця площина дістала назву комплексної.

N. B. Зверніть увагу, дійсні числа (ті числа, якими ми користуємося в побуті) на комплексній площині відповідають виключно осі абсцис. Для них y = 0 . Введення поняття комплексних чисел неймовірно розширило межі математичних обчислень. Це наче інша реальність, новий вимір. На комплексній площині ці числа — все, що лежить вище і нижче від осі абсцис. Іншими словами, з точки зору математики дійсні (звичайні) числа — це радше виняток. Переважна більшість значень виражається саме комплексними, а не дійсними числами.

Ось тепер ми нарешті підібрались упритул до множини Мандельброта.

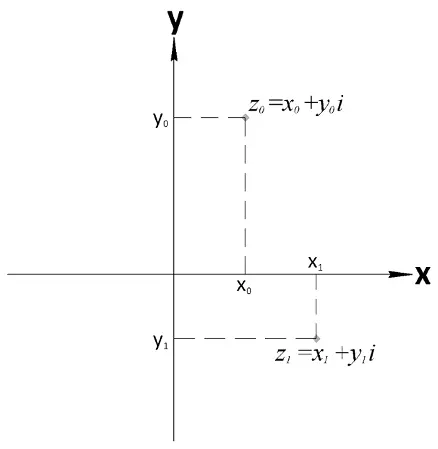
Геометричне представлення комплексних чисел на комплексній площині