Дэвид Элкиатор - Иллюстрированные принципы пула и бильярда

Как правило, угол отражения для удара от борта равен углу падения ( Рисунок 76).

• Это утверждение неверно для сильных и тихих ударов, для случаев, когда прицельный шар стоит близко к борту, для ударов с боковым вращением и для ударов на резке.

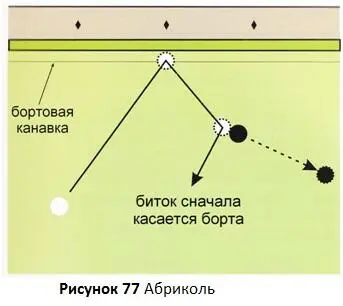
Когда биток отражается от борта перед контактом с прицельным шаром ( Рисунок 77), такой удар называется абриколь. Иногда такие удары - это единственный способ забить шар и довольно часто единственный вариант игры при хорошо выполненном отыгрыше. К счастью, все методы, используемые для прицеливания обычного удара от борта, также могут быть использованы для планирования абриколей, хотя для абриколей у вас больше возможностей для контроля вращения битка во время контакта битка с бортом.

Существует масса различных методов для прицеливания ударов от бортов и абриколей. Существуют методы, основанные на базовых принципах геометрии. Наиболее общие и практические методы включают в себя следующее:

• Метод равных отрезков

• Расширенный метод равных отрезков

• Метод параллели, проведённой через середину отрезка

• Метод зеркального отражения

• Метод равных отрезков для абриколей

Основной метод прицеливания ударов от бортов показан на Рисунке 78.

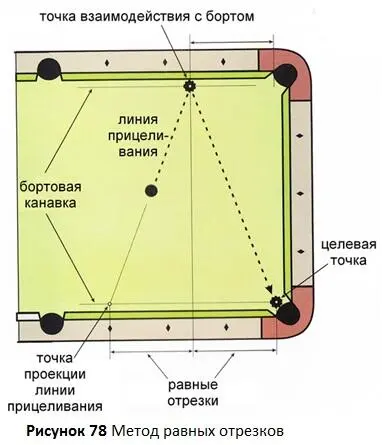Он называется Метод равных отрезков. Чтобы использовать данный метод, перемещайте точку взаимодействия с бортом вдоль борта пока не добьётесь равенства отрезков, как показано на рисунке. Отрезки можно откладывать как на борту, от которого будет отражаться прицельный шар, так и на противоположном борту, прилегающем к целевой лузе. Должно быть равенство расстояний между точкой проекции линии прицеливания и точкой взаимодействия с бортом и между точкой взаимодействия с бортом и целевой точкой. Обратите внимание, что все точки находятся на бортовых канавках, что очень важно для точного измерения расстояний.

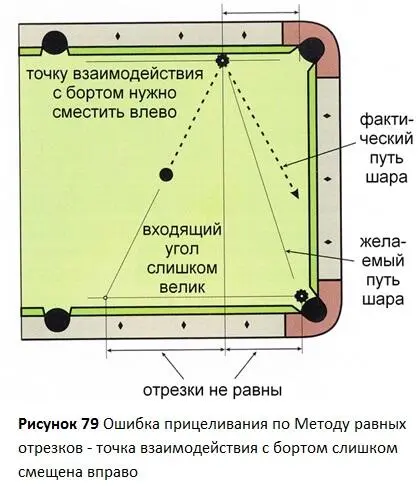
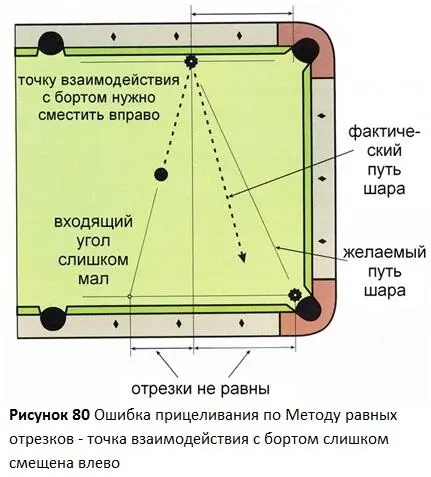
Принцип 22 Метод равных отрезков

Для удара от борта со средней скоростью, без использования винтов, следующие расстояния должны быть равны:

1. Между точкой проекции линии прицеливания и точкой взаимодействия с бортом.

2. Между точкой взаимодействия с бортом и целевой точкой.

• Равенство отрезков не будет соблюдаться для быстрых или медленных скоростей, или в случае близости прицельного шара к борту, или в случае использования винтов, или для ударов на резке.

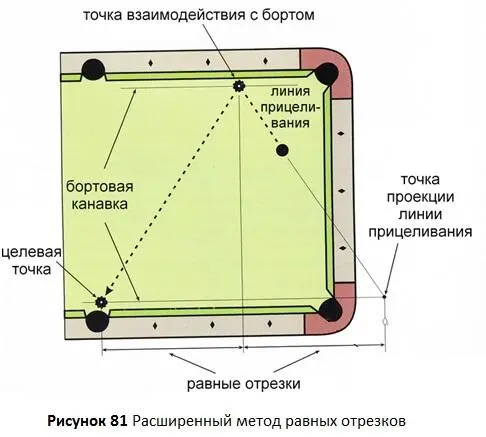Метод равных отрезков, представленный выше, может также использоваться для ударов, когда линия прицеливания, спроектированная назад, выходит за пределы стола. На Рисунке 81показан такой случай. Метод прицеливания, применяемый для таких ударов, на самом деле такой же, как Метод равных отрезков. Но когда вам нужно измерить расстояние за пределами стола, я называю этот способ Расширенным методом равных отрезков. Как и прежде, вы смещаете точку взаимодействия с бортом, пока не добьётесь равенства отрезков, проведённых между точкой проекции линии прицеливания, точкой взаимодействия с бортом и целевой точкой.

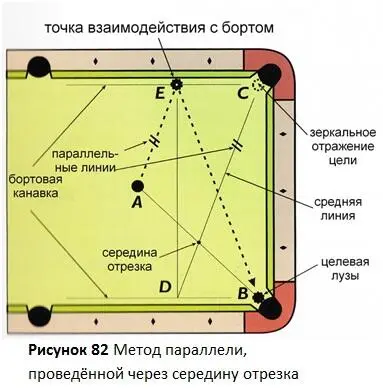Альтернативой Методу равных отрезков служит метод, показанный на Рисунке 82. Он называется Метод параллели, проведённой через середину отрезка. Этот метод концептуально немного сложнее, чем Метод равных отрезков, но он прост и не требует догадок и корректировок относительно точки взаимодействия с бортом.

Для использования метода, сначала представьте отрезок между текущим положением прицельного шара (точка А) и целевой лузой (точка B). Далее разделите отрезок АВ пополам, чтобы найти середину отрезка. Затем представьте себе линию (например, при помощи кия) через эту середину отрезка и зеркальное отражение целевой лузы на другой стороне стола (точкой С). Эта линия (отрезок DC) обозначена на рисунке как "средняя линия". Она задаёт направление, по которому прицельный шар должен приближаться к борту из точки А, чтобы отразиться от борта (в точке взаимодействия с бортом Е) и попасть в лузу (в точку В). То есть, прямая АЕ параллельна средней линии DC. Точка взаимодействия с бортом (точка Е) может быть найдена с помощью проекции точки D на противоположный борт. Этот метод включает в себя несколько шагов и требует умения визуализировать различные линии и находить середину отрезка, но он может быть хорошей альтернативой Методу равных отрезков.