Юрий Подольский - Резьба по дереву. Техники, приемы, изделия

Деление на 6 и 12 частей(рис. 12, е ). Из точек пересечения окружности с вертикальным диаметром проводят две дуги, радиус которых равен радиусу окружности. Пересечение дуг на окружности образует точки, которые последовательно соединяются хордами. В результате образуется вписанный в окружность шестиугольник. Для разделения окружности на 12 частей делают такое же построение, но только на двух взаимно перпендикулярных диаметрах.

Деление на 7 частей(рис. 12, ж ). Из конца любого диаметра проводят вспомогательную дугу радиусом R . Через точки ее пересечения с окружностью проводят хорду, равную стороне правильно вписанного треугольника (как на рис. 12, а ). Половина хорды равняется стороне вписанного в окружность семиугольника. Теперь достаточно последовательно отложить на окружности несколько дуг радиусом, равным половине хорды, чтобы разделить окружность на 7 частей.

Деление на любое количество частей(рис. 13). В данном случае окружность разделена на 9 частей.

Через центр окружности проводят две взаимно перпендикулярные прямые. Один из диаметров, например CD , по линейке делят на нужное количество равных частей (в данном случае 9), точки нумеруют. Далее из точки D проводят дугу радиусом, равным диаметру данной окружности (2 R ), до пересечения с перпендикулярной прямой АВ . Из точек пересечения А и В проводят лучи, но так, чтобы они проходили только через четные или только через нечетные (как в данном случае) номера. При пересечении с окружностью лучи образуют точки, которые делят окружность на нужное количество частей (в данном случае 9).

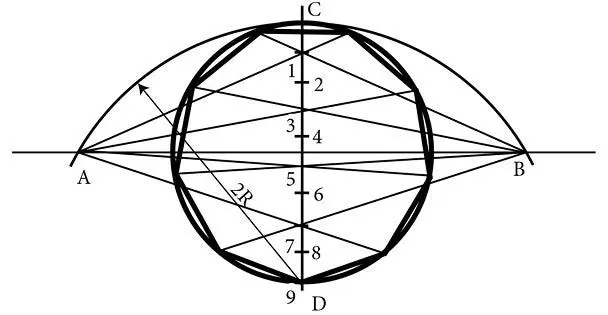
Рис. 13. Деление окружности на любое заданное количество частей.

Сопряжение двух полос разной ширины изображено на рис. 14, а . Радиус внешней дуги задается или подбирается. Точки сопряжения прямой и дуги (во всех случаях) лежат на перпендикуляре, опущенном из центра дуги на прямую. Заметим кстати, что точки сопряжения двух любых дуг находятся на линии, соединяющей их центры.

Построение окружности небольшого диаметра производят с помощью циркуля, что не вызывает затруднений. В то же время возможность построения окружности большого диаметра ограничена размером циркуля. Выйти из затруднения поможет комбинация из карандаша, нити и гвоздя (рис. 14, б ). Радиус окружности в этом случае регулируется длиной нити.

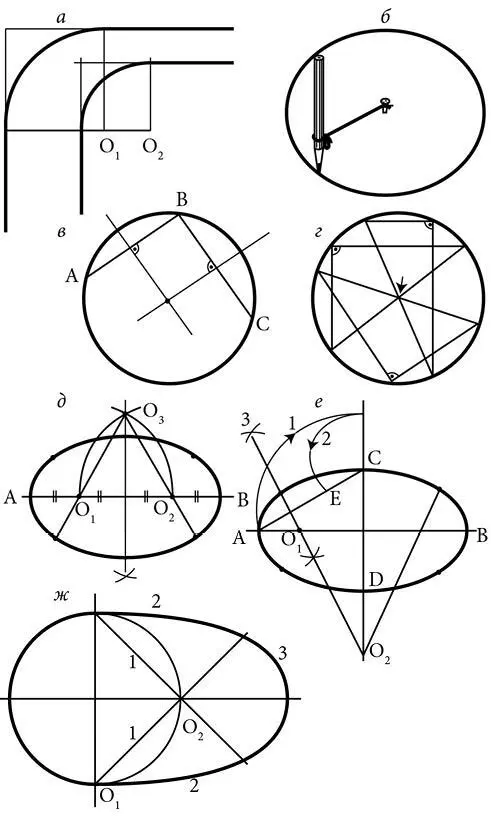
Рис. 14. Сопряжения, окружности и овалы: а – выполнение сопряжения линий; б – построение окружности большого диаметра; в – определение центра окружности методом отрезков; г – определение центра окружности с помощью прямоугольных треугольников; д – построение овалов в пропорции золотого сечения; е – построение овалов по заданным осям; ж – построение овоида.

Один из способов определения центра окружности представлен на рис. 14, в : на окружности выбирают любые три точки ( А, В , и С ), соединяют их двумя или тремя отрезками и делят эти отрезки пополам с помощью перпендикуляра к ним. Точка пересечения перпендикуляров является центром окружности. Чем ближе отрезки к диаметру окружности, тем точнее получится результат построения.

Второй способ (рис. 14, г ) основан на том, что любой прямой угол, вершина которого находится на окружности, опирается на ее диаметр. Несколько таких прямых углов, построенных с помощью угольника, определят центр окружности – это будет точка пересечения гипотенуз прямоугольных треугольников.

Подобное построение удобно для определения центров на больших окружностях или на торцах цилиндров, например на спилах ствола дерева. Построение будет точнее, если гипотенузы треугольников пересекаются под углом, близким к прямому.

В обоих случаях найденный центр окружности желательно проверить с помощью циркуля.

Существует несколько способов построения овалов. Один из них заключается в сопряжении дуг. Если овал задан его длиной, то построение лучше делать в пропорции золотого сечения, как показано на рис. 14, д . Отрезок АВ делят на четыре части, в результате чего образуются точки О 1 и О 2. Центр О 3 получается в точке пересечения дуг из О 1 и О 2 радиусом, равным величине отрезка О 1 О 2. Чтобы построить более широкий овал, отрезок АВ необходимо разделить на 3 части.